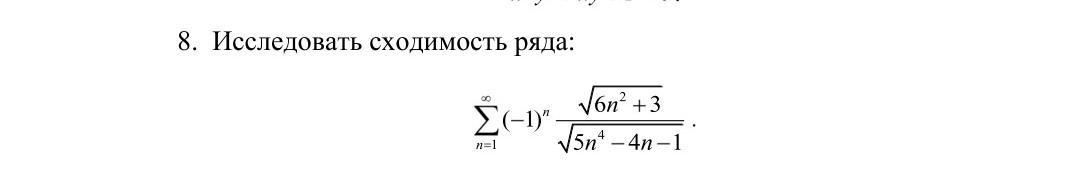Question

Помогите пожалуйста решить ​

Answer 1

Ряд имеет вид $\sum\limits_{n=1}^{\infty}(-1)^{n}a_{n},\; a_{n}\geq 0$. Заметим, что $a_{n}$ в нашем случае является монотонно убывающей к нулю последовательностью. В самом деле, для того чтобы увидеть монотонность, перейдем к функции $f(x) = \sqrt{\dfrac{6x^2+3}{5x^4-4x-1}} \Rightarrow \mathrm{sgn} f'(x) = \mathrm{sgn}\left(\dfrac{6x^2+3}{5x^4-4x-1}\right)' =\\= \mathrm{sgn}\left(\dfrac{12x}{5x^4-4x-1}- \dfrac{(6x^2+3)(20x^3-4)}{(5x^4-4x-1)^2}\right)$. Осталось заметить, что $12x(5x^4-4x-1)<(6x^2+3)(20x^3-4),\; \forall x\geq x_{0}$, где $x_{0}$ достаточно велико, поскольку слева при $x^5$ стоит коэффициент $60$, а справа -- $120$. Значит, начиная с некоторого номера $f'(x) < 0 \Rightarrow a_{n}\downarrow$.

Ясно также, что $\lim\limits_{n\to\infty} a_{n} = 0$, значит, ряд сходится по признаку Лейбница.