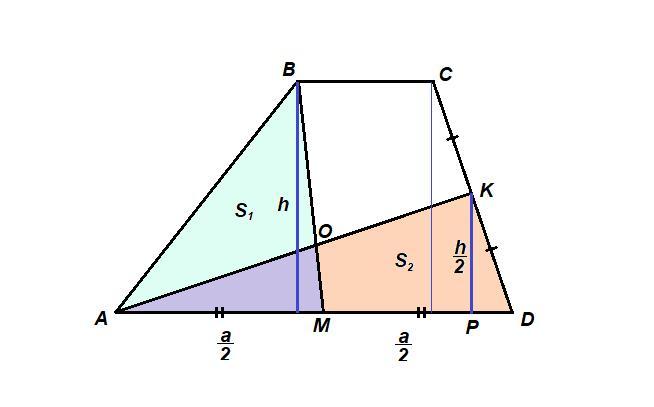
отмеченные на рисунке точки -- середины сторон трапеции. Докажите, что площади закрашенных фигур равны.
Приложения:

Ответы
Ответ дал:
5
Ответ:
Обозначим основание AD = а, высоту ВН = h.
по теореме Фалеса.
Площадь треугольника АВМ:
Площадь треугольника AKD:
Значит, .
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад