найдите общий вид на указанном промежутке. Спасибо.
Приложения:
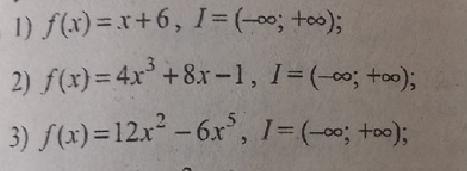
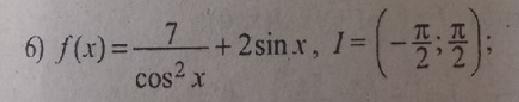
NNNLLL54:
общий вид чего ???
Для данной функции f найдите общий вид первообразны на указанном промежутке I
Спасибо БОЛЬШОЕ!!!!!
Ответы
Ответ дал:
2
Ответ:
F(x) - первообразная функции y=f(x) .
и еще сможете пожалуйста задачу решит?) https://znanija.com/task/47585909
СПАСИБО БОЛЬШОЕ!!!!
здесь ещё спасибо не нажал ...
кнопочка есть
вот эту поможете? https://znanija.com/task/47585909
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад