ПОМОГИТЕ ПОЖАЛУЙСТА НАЙТИ ПРОИЗВОДНУЮ
исследуйте функцию на монотонность и экстремумы функцию
Приложения:
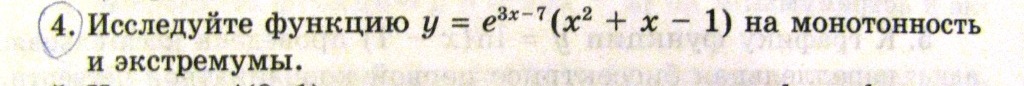
Ответы
Ответ дал:
0
Для нахождения производной произведения есть формула:
(f(х)*g(x))'= f '(x)* g(x) + f(x)*g'(x)
Таким образом,
y'= 3e^3x-7 * (x^2+x-1) + e^3x-7 * (2x+1)
Можно еще вынести за скобку множитель e^3x-7, тогда
y'= e^3x-7 (3x^2+3x-3+2x+1)= e^3x-7 (3x^2+5x-2)
(f(х)*g(x))'= f '(x)* g(x) + f(x)*g'(x)
Таким образом,
y'= 3e^3x-7 * (x^2+x-1) + e^3x-7 * (2x+1)
Можно еще вынести за скобку множитель e^3x-7, тогда
y'= e^3x-7 (3x^2+3x-3+2x+1)= e^3x-7 (3x^2+5x-2)
Ответ дал:
0
ставим найденные в уравнении точки на координатной прямой, определяем знакочередование производной, в промежутках справа налево получаем: "+", "-", "+". Те точки, где производная меняет знак с плюса на минус - это точки максимума функции, в нашем случае точка максимума одна - это точка -2. Там, где производная меняет знак с минуса на плюс - точки минимума, у нас это 1/3
Ответ дал:
0
На тех промежутках, где стоит "+" - функция возрастает, а где "-" - убывает
Ответ дал:
0
поэтому наша функция возрастает на промежутке от (-бесконечности; -2) и на (1/3; +бесконечности), а убывает на (-2; 1/3)
Ответ дал:
0
всё. с ответом сошлось. спасибо огромное!!))
Ответ дал:
0
пожалуйста :)
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад