Question

найти стороны AQ, AC, MN, PN пожалуйста!!​

Answer 1

Ответ:

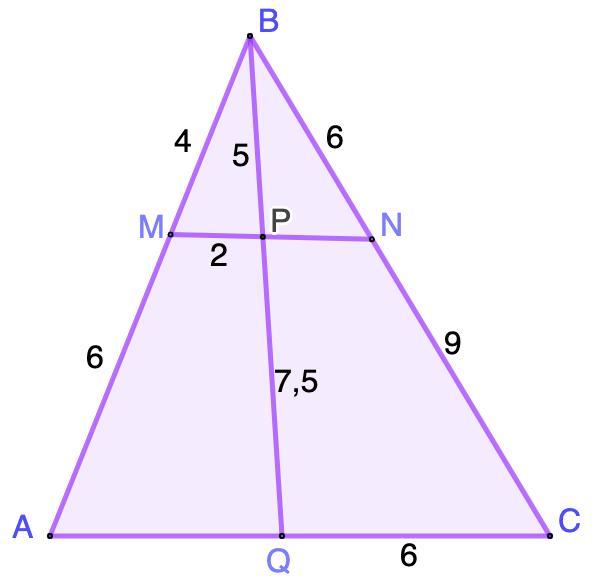
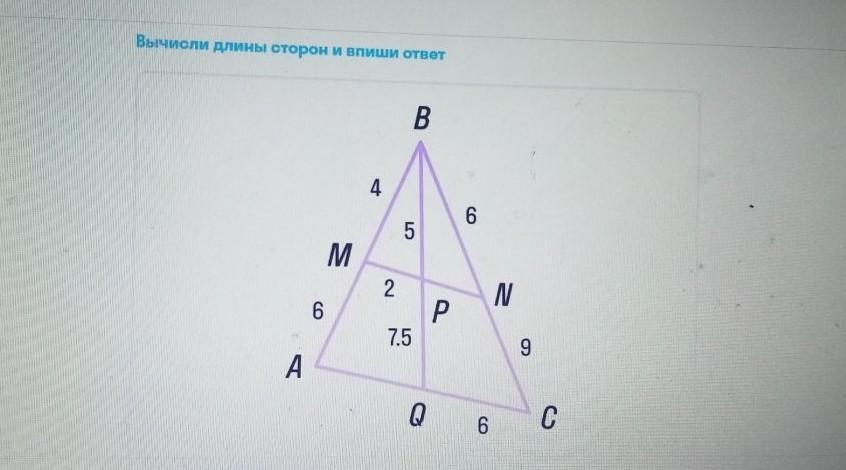
AQ = 5 (ед.)

AC = 11 (ед.).

MN = 4,4 (ед.)

PN = 2,4 (ед.)

Пошаговое объяснение:

Требуется найти стороны AQ, AC, MN, PN.

Дано: ΔАВС.

АМ = 6; МВ = 4; BN = 6; NC = 9;

BP = 5; PQ = 7,5; MP = 2.

Найти: AQ, AC, MN, PN.

Решение:

1. Докажем, что MN || AC.

Воспользуемся обратной теоремой Фалеса:

• Если две или более прямых  отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные.

Проверим пропорциональность отрезков:

$\displaystyle \frac{BM}{BN}=\frac{AM}{NC} \\\\\frac{4}{6}=\frac{6}{9} =\frac{2}{3}$

⇒ отрезки пропорциональны, а значит

MN || AC

2. Найдем сторону AQ.

Рассмотрим ΔМВР и ΔABQ.

MP || PQ

• Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒  ΔМВР ~ ΔABQ.  

Составим отношения сходственных сторон и найдем AQ:

$\displaystyle \frac{BM}{AB} =\frac{MP}{AQ} \\\\\frac{4}{4+6}= \frac{2}{AQ}\\ \\AQ=\frac{10*2}{4} =5$

Сторона AQ = 5 (ед.).

3. Найдем сторону  АС.

AC = AQ + QC = 5 + 6 = 11 (ед.).

4. Найдем сторону MN.

Рассмотрим ΔMBN и ΔАВС.

MN || AC

⇒ ΔMBN ~ ΔАВС  (лемма)

Составим отношения сходственных сторон и найдем MN:

$\displaystyle \frac{BM}{AB} =\frac{MN}{AC}\\ \\\frac{4}{10}=\frac{MN}{11}\\ \\ MN=\frac{4*11}{10} =4,4$

MN = 4,4 (ед.)

5. Осталось найти сторону PN.

PN = MN - MP = 4,4 - 2 = 2,4 (ед.)