Question

Доведіть, що (4-a)(a+2)<2(21-4a) при всіх дійсних значеннях a

Answer 1

Ответ:

Объяснение:

(4-a)(a+2)=4а+8-а²-2а=-а²-2а+8 це парабола обернута до низу

знайдемо її максимум. Візьмемо похідну та    = 0

(-а²-2а+8)'=-2а-2=0 ⇒ а=-1 найбільше значення

Підставимо а=-1 у другий вираз

2(21-4a)=42-8*(-1)=50  

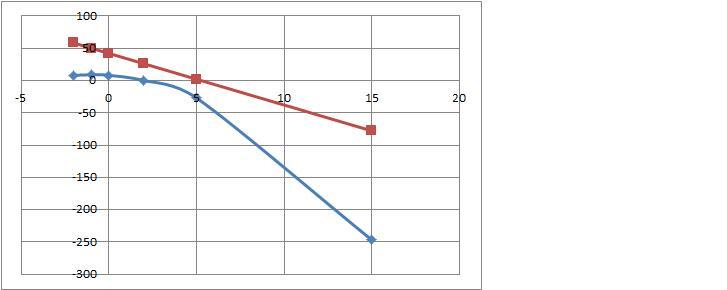
якщо зробити графік побачимо, що ці графікі не перетинаються і рівняння виконується при всіх дійсних значеннях a