Question

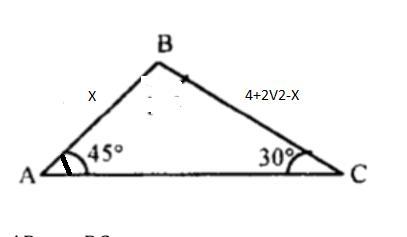
Дан треугольник ABC. Если AB + BC = (4 +2√2) см, ∠A = 45° см и ∠C = 30°, то найди длину радиуса окружности, описанной около данного треугольника.​

Answer 1

Ответ:

R=2√2

Объяснение:

По т. синусов

решение на фото

Answer 2

Вариант решения.

Ответ: 2√2 см

Объяснение:

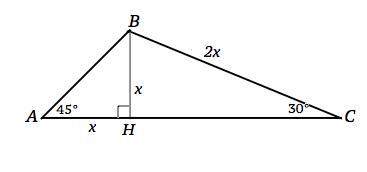
  Опустим из вершины В высоту до пересечения с основанием АС в точке Н.

Треугольник ВНС - прямоугольный с катетом ВН, противолежащим углу 30°.

Примем ВН=х. Тогда ВС=ВН:sin30°=х:1/2=2х

АВ=х:sin45°=x:(√2/2)=x√2

По условию AB + BC = (4 +2√2) =>

х√2+2х = (4 +2√2) =>

х•(√2+2)=2(√2+2) =>

х=2 см;  BC=2x=4 см

По т.синусов 2R=ВС:sin45°

2R=4:√2/2=4√2 =>

R=2√2 см