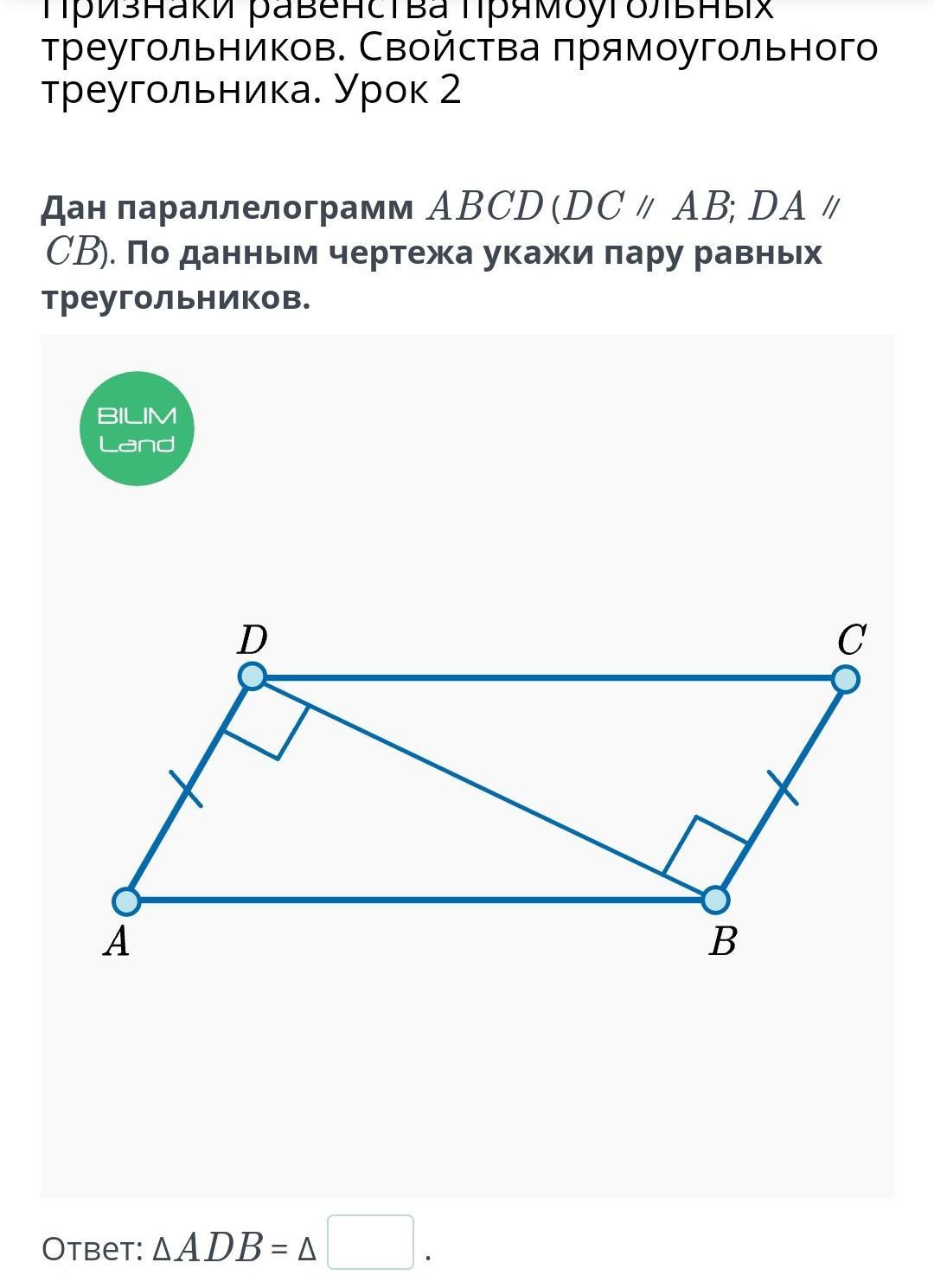
Дан параллелограмм ABCD (DC ∥ AB; DA ∥ CB). По данным чертежа укажи пару равных треугольников.
Ответ: ∆ADB = ∆
Приложения:
Ответы
Ответ дал:
4
Ответ:
∠ADB = ∠CDB
Объяснение:
Данные треугольники имеют общий элемент - катет BD. Также, по условию задачи, у них есть пара равных сторон AD = BC, которые являются катетами в данных треугольниках.
Следовательно, треугольники равны по двум катетам.
Осталось записать вершины равных треугольников в верной последовательности: ∠ADB = ∠CBD = 90°, ∠ABD = ∠CDB, как внутренние накрест лежащие при DC ║ AB, DB - секущая. Отсюда ∠A= ∠C.
Получаем: ∠ADB=∠CBD.
Вас заинтересует
1 год назад
1 год назад
2 года назад
9 лет назад