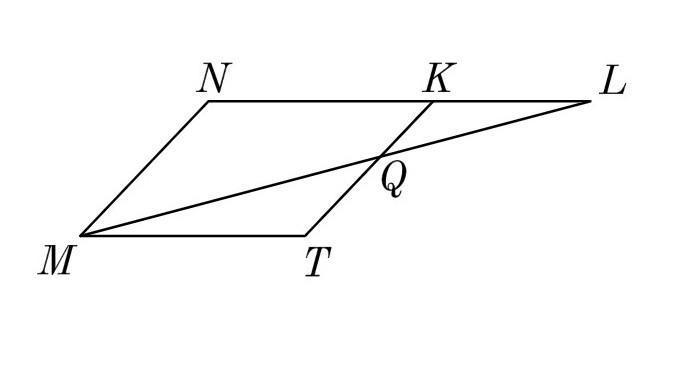
В параллелограмме MNKT точка Q делит сторону TK так, что TQ:QK=1:3. Найди стороны треугольника QKL, если
MQ =22, MT=20, TQ=5.
Приложения:
rasulserikuly:
KQ=15
спасибо
это все???
я думаю :)
если не могу то скажу
хорошо. спасибо большое
я нашёл того кто уже ответил на этот вопрос
https://znanija.com/task/47635353
вот этот
спасибо
Ответы
Ответ дал:
3
Ответ:
QK = 15 см, KL= 60 см, QL= 66 см.
Объяснение:
1) △MQT подобен △LQT по двум углам (первый признак подобия треугольников):
- ∠KQL =∠TQM - как вертикальные.
- ∠NLM =∠TML - как внутренние накрест лежащие углы при параллельных прямых NL и MT и секущей LМ.
2) Найдём коэффициент подобия.
Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
3) Так как в подобных треугольниках соответственные стороны пропорциональны, с коэффициентом пропорциональности k, найдём стороны ΔQKL:
Стороны треугольника QKL: QK = 15 см, KL= 60 см, QL= 66 см.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад