Question

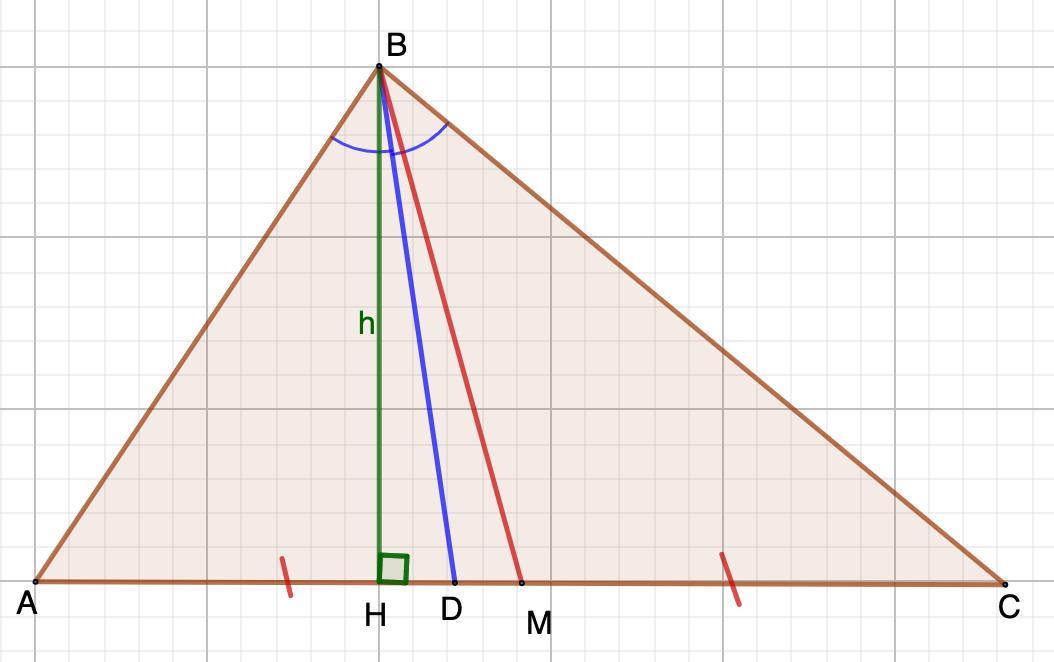
В треугольнике ABC провели биссектрису BD и медиану BM известно что AB : BC равна 3:5 и площадь треугольника ABC равна 40 найдите площадь ∆BDM

Answer 1

Ответ:

Площадь ΔBDM = 12,5 ед².

Пошаговое объяснение:

Требуется найти площадь ΔBDM.

Дано: ΔАВС;

ВD - биссектриса;

ВМ - медиана;

АВ : ВС = 3 : 5;

S (ΔABC) = 40 ед².

Найти: S (∆BDM).

Решение:

Рассмотрим ΔАВС.

1. ВМ - медиана.

• Медиана разбивает треугольник на два равновеликих (по площади) треугольника.

⇒    $\displaystyle S_{ABM}=S_{MBC} = S_{ABC}:2=40:2=20$  (ед².)

2. Проведем высоту ВН = h.

• Площадь треугольника равна половине произведения основания на высоту.

• $\displaystyle \boxed { S=\frac{1}{2}ah }$  , где а - основание, h - высота.

$\displaystyle S_{ABC}=\frac{1}{2}*AC*h\;\;\;\Rightarrow \;\;\;40=\frac{1}{2}AC *h\\ \\AC*h=80\\\\AC=\frac{80}{h}$

3. ВD - биссектриса.

Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.

⇒    $\displaystyle \frac{AB}{BC}=\frac{AD}{DC}=\frac{3}{5}$

AD = 3 части, DC = 5 частей ⇒ АС = 8частей.

Выразим AD:

$\displaystyle AD=\frac{AC*3}{8} =\frac{40*3}{h*8}=\frac{15}{h}$  (ед.)

4. Найдем площадь ΔABD.

$\displaystyle S_{ABD}=\frac{1}{2}*AD*h=\frac{1}{2}*\frac{15}{h} *h=\frac{15}{2}$   (ед².)

5. Найдем площадь Δ BDM:

$\displaystyle S_{BDM}=S_{ABM}-S_{ABD} = 20-\frac{15}{2}=\frac{25}{2}=12,5$  (ед².)

Площадь ΔBDM = 12,5 ед².