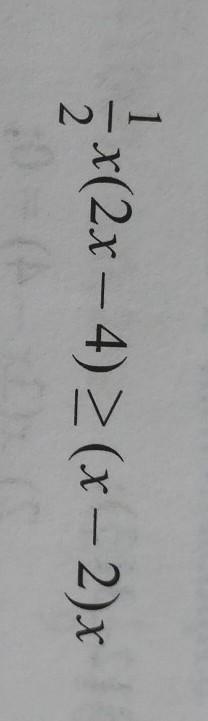Ответы
Ответ дал:
2
Ответ:
из этого следует что верно неравенство при любых значениях х
Ответ дал:
1
Выражения равны, следовательно, их значения при любом x будут равны (неравенство нестрогое, следовательно, оно всегда будет верно, несмотря на то, что знак "больше" роли в нём не играет)
1. x = 0;
0(0 - 2) ≥ 0(0 - 2)
0 = 0
2. x ≠ 0;
Исходное неравенство допускает оба исхода
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
9 лет назад