Найти все частные производные данной функций по каждой из независимых переменных
z=(y/x)^x
Приложения:
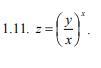
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад