найти все натуральные значения n удовлетворяющие уравнению 2022*[n*sqr(1011^2+1)]=n*[2022*sqr(1011^2+1)] , где [х] - наибольшее целое числоне превосходящее числа.
Ответы
Ответ дал:
2
Пусть . Заметим, что
, поэтому
. Тем самым уравнение перепишется в виде
.
Теперь подход примерно такой же: . Если
, то равенство выполняется. Пусть
. Тогда
, значит, равенство выполняться уже не будет. Получаем, что решениями будут натуральные числа
.
Guerrino:
латех на этом сайте, конечно, максимально убогий...
Ответ дал:
2
Ответ:
Пошаговое объяснение:
Заметим:
Отсюда
Но это означает, что
Значит, уравнение равносильно
Если решения данного уравнения существуют, то, по определению дробной части числа, верно неравенство
Но для таких значений переменной верны неравенства
по определению целой части числа равенство
верно. Значит, все натуральные значения
являются корнями данного уравнения.
Приложения:
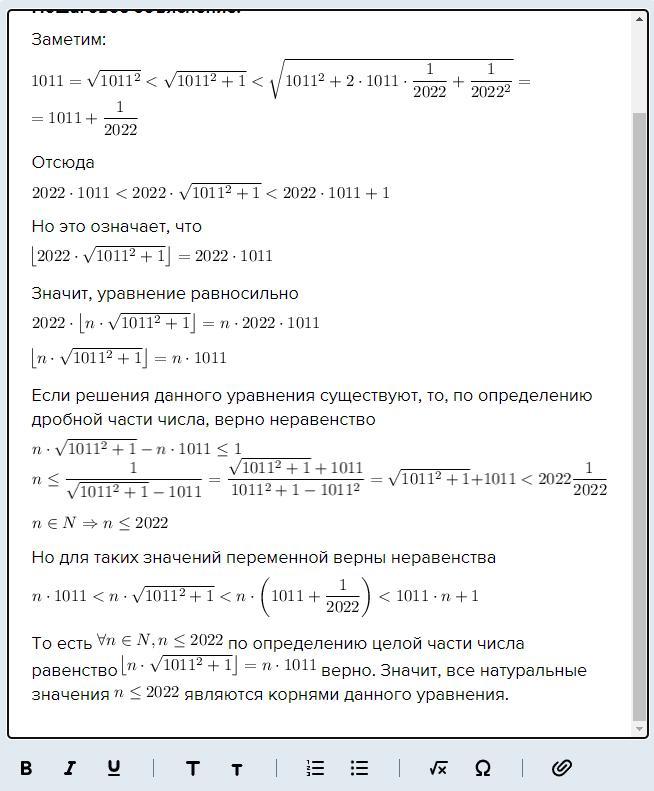
Какие-то проблемы с редактором, не дает нормально оформить конец ответа
Прикрепил скриншот окна ответа с корректным отображением, передам ошибку техподдержке
Вас заинтересует
2 года назад
3 года назад
8 лет назад
8 лет назад