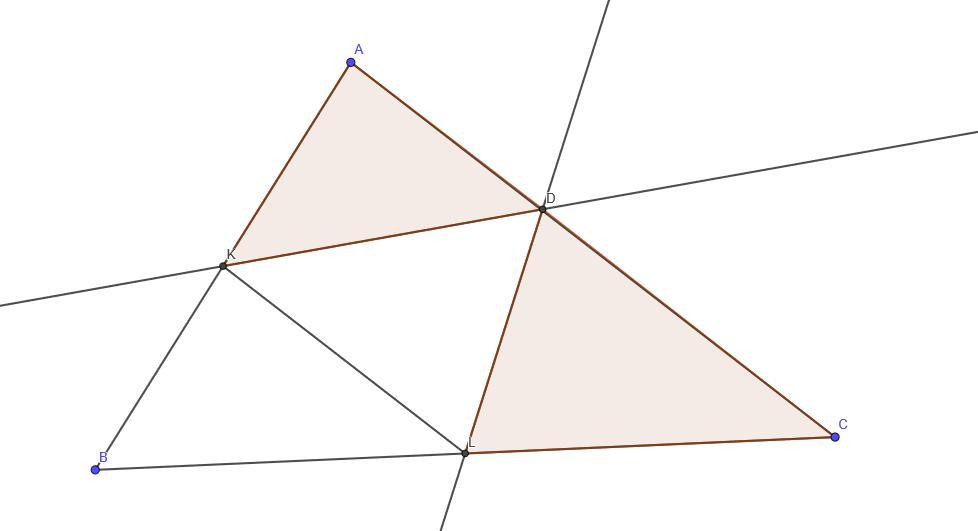
Дан треугольник ABC. Точки K и L — середины сторон AB и BC соответственно. Оказалось, что биссектрисы углов AKL и CLK пересекаются на отрезке AC. Найдите длину отрезка AC, если известно, что AB=17 и BC=24.
Ответы
Ответ дал:
3
Ответ:
20,5
Объяснение:
Точки K и L — середины сторон AB и BC соответственно.
KL - это средняя линия.
- Средняя линия параллельна противолежащей стороне и равна ее половине.
KL || AC
- ∠AKD=∠LKD - по условию
- ∠KLD=∠DLC - по условию
∠LKD=∠KDA - как накрест лежащие углы при KL || AC и секущей KD
∠KLD=∠LDC - как накрест лежащие углы при KL || AC и секущей LD
Значит, ∠AKD=∠LKD=∠KDA и ∠KLD=∠DLC=∠LDC
⇒ ΔAKD и ΔCDL - равнобедренные ⇒ KA=AD, LC=CD
Значит, KA=AD=BK, LC=CD=BL
AC=AD+CD=(1/2)·AB + (1/2)·BC=(1/2)·(AB+BC)=(1/2)·41=20,5
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад