Question

................................​

Answer 1

Ответ:

$\boxed{\ sin^2a+cos^2a=1\ \ \Rightarrow \ \ \ sin^2a=1-cos^2a\ ,\ \ cos^2a=1-sin^2a\ }$

$\boxed{\ tga\cdot ctga=\frac{sina}{cosa}\cdot \frac{cosa}{sina}=1\ \ ;\ \ 1+tg^2a=1+\frac{sin^2a}{cos^2a}=\frac{sin^2a+cos^2a}{cos^2a}=\frac{1}{cos^2a}\ }$

$\displaystyle \frac{cos^2a-1}{1-sin^2a}-tga\cdot ctga=\frac{-(1-cos^2a)}{cos^2a}-1=\frac{-sin^2a}{cos^2a}-1=-tg^2a-1=\\\\=-(1+tg^2a)=-\frac{1}{cos^2a}$

Answer 2

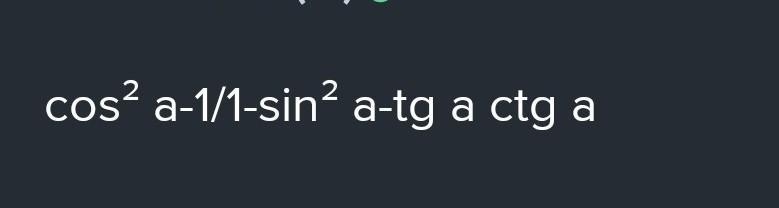
Ответ:-1/cos²α

Объяснение:приведем к общему знаменателю выражение, упростим числитель, воспользуемся основным тригонометрическим тождеством cos²α+sin²α=1, а также тождеством tgα*ctgα=1;тождеством

1-sin²α=сos²α,

получим: (cos²α-1)/(1-sin²α)-tgα*ctgα=(cos²α-1-1*(1-sin²α))/(1-sin²α)=

(cos²α-1-1+sin²α)/(1-sin²α)=(-2+1)/cos²α=-1/cos²α