Question

Помогите пожалуйста, нужно решить за 1.5 часа, зарание спасибо.
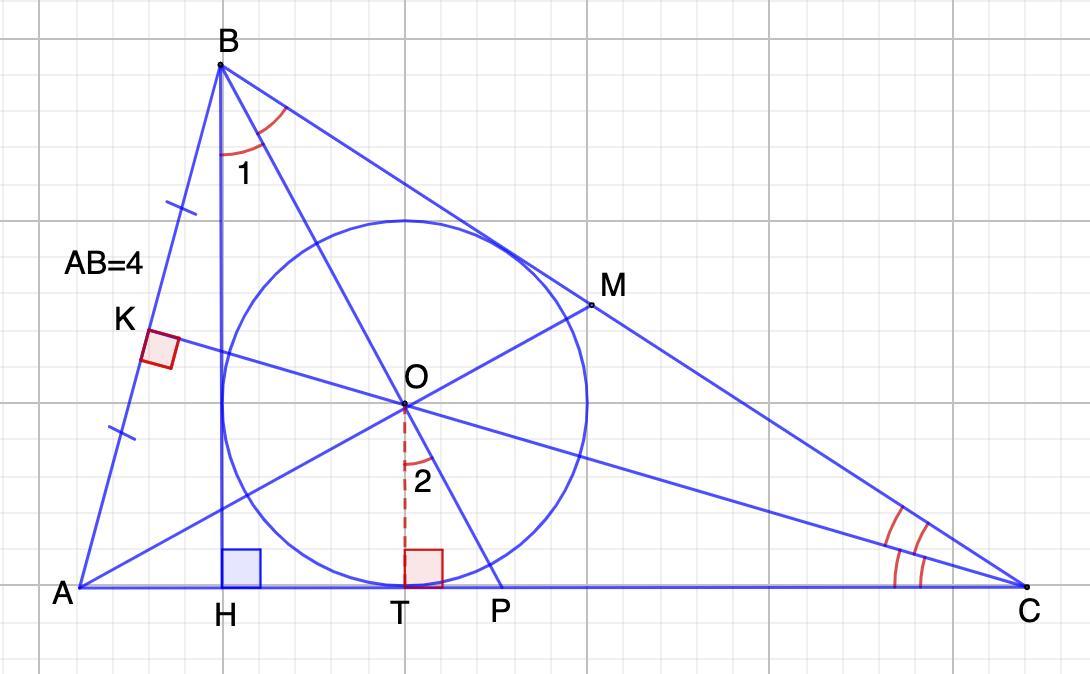
В остроугольном треугольнике ABC точка H — основание высоты из точки B. Оказалось, что центр вписанной окружности треугольника BCH совпадает с точкой пересечения медиан треугольника ABC. Найдите AC2, если AB=4.

Answer 1

Ответ:

Нашли AC² = 40 (ед².)

Пошаговое объяснение:

Требуется найти АС².

Дано: ΔАВС - остроугольный;

ВН - высота;

Окр.О - вписана в ΔВСН;

ВР, СК, АМ - медианы ΔАВС.

О - точка пересечения медиан.

АВ = 4.

Найти: АС².

Решение:

Проведем радиус ОТ.

1. Рассмотрим ΔНВР и ΔТОР.

∠ВРН - общий.

ВН ⊥ НР (условие)

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОТ ⊥ НТ

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ ВН || ОТ

∠1 = ∠2 (соответственные при ВН || ОТ и секущей ВР.

• Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

⇒  ΔТОР ~ ΔНВР

• Медианы треугольника точкой пересечения делятся в отношении 2:1, начиная от вершины.

Если ОР = 1 часть, то ОВ = 2 части, тогда ВР = 3 части.

Составим отношение сходственных сторон:

ОТ : ВН = ОР : ВР = 1 :3

Пусть ОТ = х, тогда ВН = 3х.

2. Рассмотрим ΔАВН - прямоугольный.

По теореме Пифагора:

АН² = АВ² - ВН²

$\boxed {AH=\sqrt{4^2-(3x)^2}=\sqrt{16-9x^2}}$

3. НС = АС - АН

$\boxed {HC=AC-\sqrt{16-9x^2}}$

4. Рассмотрим ΔАВС.

СК - медиана (условие)

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ СК - биссектриса.

• Если в треугольнике медиана является биссектрисой, то этот треугольник равнобедренный.

⇒ ΔАВС - равнобедренный, то есть АС = ВС.

• В равнобедренном треугольнике медиана является высотой.

⇒ СК - высота.

5. Рассмотрим ΔНВС - прямоугольный.

• Радиус вписанной окружности в прямоугольный треугольник вычисляется по формуле:
• $\displaystyle \boxed {r=\frac{a+b-c}{2} }$ , где а и b - катеты, с - гипотенуза.

Подставим значения:

$\displaystyle OT=\frac{BH+HC-BC}{2} \\\\2x=3x+(AC-\sqrt{16-9x^2})-AC\\ \\x=\sqrt{16-9x^2}$

Возведем в квадрат обе части:

$\displaystyle x^2=16-9x^2\\\\10x^2 = 16\\\\x=\sqrt{1,6}$

⇒ ВН = 3х = 3√1,6

6. Рассмотрим ΔАКС - прямоугольный;

AK = AB : 2 = 2 (СК - медиана)

По теореме Пифагора:

$KC^2=AC^2-AK^2\\\\KC=\sqrt{AC^2-4}$

7. Выразим площадь ΔАВС двумя способами:

• Площадь треугольника равна половине произведения основания на высоту.

$\displaystyle S_{ABC}=\frac{1}{2} AB*KC=\frac{1}{2}AC*BH$

или

$\displaystyle AB*KC=AC*BH\\\\4*\sqrt{AC^2-4}=AC*3\sqrt{1,6}$

Возведем в квадрат обе части:

$\displaystyle 16*(AC^2-4)=AC^2*9*1,6\\\\16AC^2-64=14,4AC^2\\\\1,6AC^2=64\\\\\boxed {AC^2=40}$

Нашли AC² = 40 (ед².)