Question

А) Дан равнобедренный треугольник ΔMKN, в котором
угол ∠N = 70° и ML – биссектриса угла ∠M. Найдите значение углов ∠KLM и ∠NLM.

Б) В треугольнике ABC провели биссектрису BF. Найдите угол C, если ∠A = 49°, ∠AFB = 68°.
В) ∠BCD – один из внешних углов треугольника равен 136°, а B – один из углов треугольника, не смежный с ним, равен 61°. Найдите второй угол A треугольника, не смежный с данным внешним. Запишите только ответ.
Ответ: ∠A = ____________°.
Г) Дан равнобедренный треугольник ΔABC. Отрезок ОК проведен таким образом, что KO = OB и ∠KOB – прямой. Найдите значения углов ∠BAC, ∠BCA, ∠ABC.

Answer 1

Ответ:

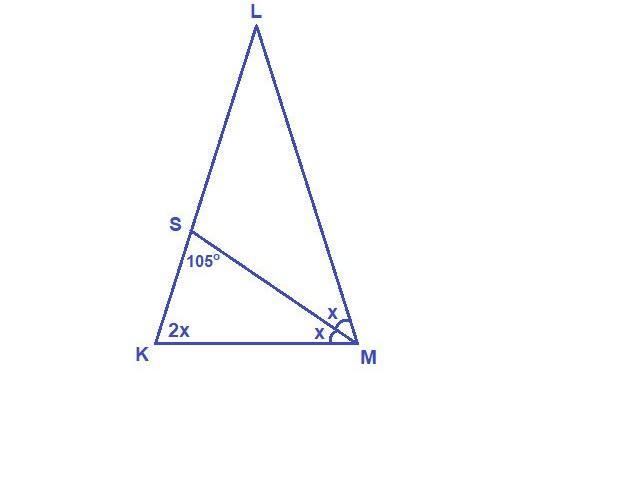
Обозначим половины угла KML переменной х.

Тогда ∠KML = 2x.

Углы при основании равнобедренного треугольника равны, значит

∠SKM = ∠KML = 2x.

ΔSKM: ∠SKM = 2x, ∠SMK = x, ∠MSK = 105°, сумма углов треугольника равна 180°, получаем уравнение

x + 2x + 105° = 180°

3x = 180° - 105°

3x = 75°

x = 25°

∠SMK = 25°

∠LMK = ∠LKM = 25° · 2 = 50°

∠KLM = 180° - (∠LMK + ∠LKM) = 180° - 2 · 50° = 80°