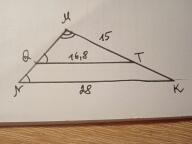
В треугольнике MNK провели прямую, параллельную стороне NK так, что она пересекает стороны MK и MN в точках Q и T соответственно.
Найди длину стороны MN , если NK=28 , TQ=16,8 , MT=15 .
Ответы
Ответ дал:
3
Ответ:
25 ед.
Объяснение:
ΔNMK подобен Δ QMT (∠М-общий, ∠MNK=∠MQT - как внутренние накрест лежащие при NK ║ TQ и секущей МN).
Из подобия треугольников следует подобие сторон:
MK/TQ=MN/MT
MN=28*15:16,8=25 ед.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
8 лет назад