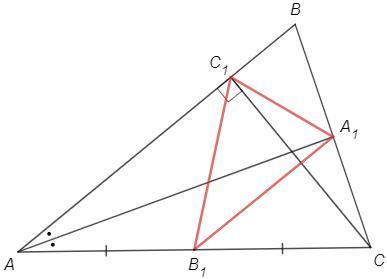
В треугольнике ABC точка A1 — основание биссектрисы, проведённой из вершины A, B1 — основание медианы, проведённой из вершины B, C1 — основание высоты, опущенной из вершины C. Оказалось, что треугольник A1B1C1 равносторонний. Докажите, что треугольник ABC также равносторонний.
Пожалуйста быстрее
Ответы
Ответ дал:
1
△ACC1: C1B1 - медиана из прямого угла равна половине гипотенузы, C1B1=AC/2
△ACA1: A1B1=C1B1 =AC/2. Медиана A1B1 равна половине стороны, следовательно проведена из прямого угла, ∠AA1C=90.
△ABC: AA1 - биссектриса и высота, следовательно и медиана, △ABC - равнобедренный, AC=AB
△CBC1: C1A1 - медиана из прямого угла, C1A1=BC/2
C1A1=C1B1 => BC=AC =AB
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад