Question

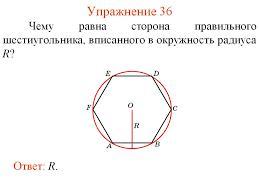
На сколько процентов площадь круга, описанного около правильного шестиугольника, больше площади круга, вписанного в этот же шестиугольник?​

Answer 1

Ответ:

25%

Пошаговое объяснение:

площадь любой окружности в 360° S=πR²;
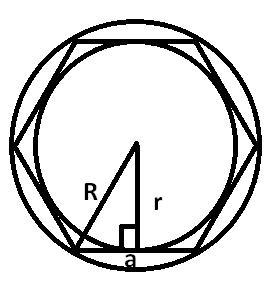
по теореме пифагора R=√r²+(1/2a)²;
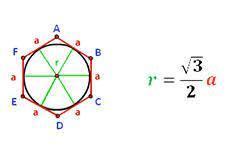
т.к. радиус описанной окружности является стороной равностороннего треугольника то высота h=r; высота правильного треугольника r=a√3/2;
R=√3a²/4+a²/4=
R=√4a²/4=√a²=a;
r=a*√3/2;
S1 описанной окружности=πR²=πa²;
S2 вписанной окружности=πr²=πa²*√3²/2²=πa²*3/4
Значит, S1=S2:(3/4); S2=(3/4)*S1=0,75*S1
Площадь описанной окружности больше площади вписанной на 1 - 3/4=1/4=0,25=25%

Незачто.