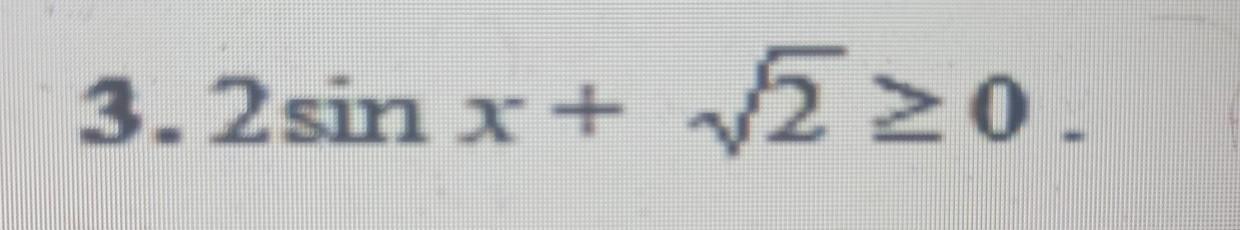Ответы
Ответ дал:
0
Ответ:
Объяснение:
Вычитаем с обеих сторон
Упрощаем
Разделим обе части на 2
Упрощаем
Упрощаем
Ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад