Question

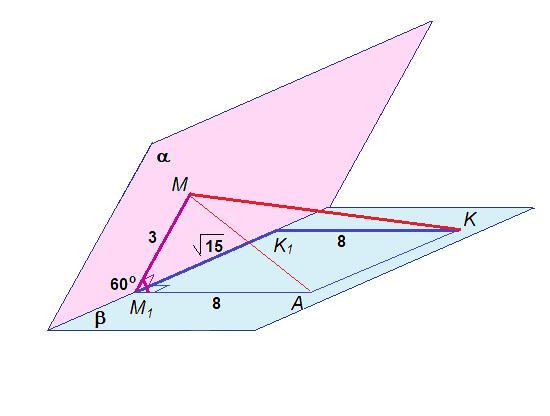
Из точек М и K, лежащих в разных гранях двугранного угла величиной 60°, проведены перпендикуляры MМ1 и KK1 к его ребру длиной 3 см и 8 см соответственно. Найти длину отрезка МK, если М1K1 = корень из 15 см.
ДАЮ 100 БАЛЛОВ

Answer 1

Ответ:

8 см

Объяснение:

Дан двугранный угол, величиной 60°.

ММ₁⊥М₁К₁,  КК₁⊥М₁К₁

ММ₁ = 3 см,  КК₁ = 8 см,  М₁К₁ = √15 см

Достроим прямоугольник AM₁K₁K на сторонах М₁К₁ и КК₁.

AM₁⊥M₁K₁ и ММ₁⊥М₁К₁, значит

∠ММ₁А = 60° - линейный угол двугранного угла между плоскостями.

АМ₁ = КК₁ = 8 см

ΔММ₁А: по теореме косинусов

AM² = MM₁² + AM₁² - 2·MM₁·AM₁·cos∠MM₁A

AM² = 3² + 8² - 2 · 3 · 8 · cos 60°

AM² = 9 + 64 - 2 · 24 · 0,5 = 73 - 24 = 49

AM = 7 см

АМ₁⊥АК как стороны прямоугольника,

Наклонная АМ проецируется на прямую АМ₁, значит

АМ⊥АК по теореме о трех перпендикулярах.

ΔМАК:  ∠МАК = 90°,  АК = М₁К₁ = √15 см

по теореме Пифагора:

МК = √(АМ² + АК²) = √(7² + (√15)²) = √(49 + 15) = √64 = 8 см