Question

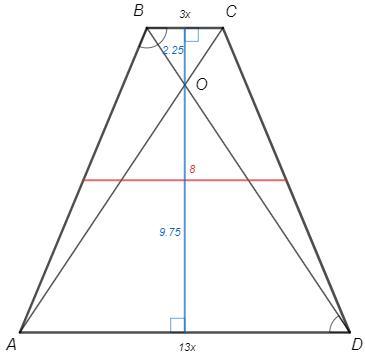
У рівнобічній трапеції діагоналі є бісектрисами тупих кутів. Відстані від точки перетину діагоналей до основ трапеції дорівнюють 2,25 см і 9,75 см. Знайдіть периметр трапеції, якщо середня лінія дорівнює 8 см.
(рус. В равнобокой трапеции диагонали являются биссектрисами тупых углов. Расстояния от точки пересечения диагоналей к основаниям трапеции равны 2,25 см и 9,75 см. Найдите периметр трапеции, если средняя линия равна 8 см.)

Answer 1

∠ABD=∠CBD (BD - биссектриса)

∠ADB=∠CBD (накрест лежащие при BC||AD)

=> ∠ABD=∠ADB => △BAD - равнобедренный

=> AB=AD=CD

△BOC~△AOD (по накрест лежащим при BC||AD)

Расстояние измеряется длиной перпендикуляра.

2,25 и 9,75 - высоты к основаниям треугольников BOC и AOD.

В подобных треугольниках отношение соответствующих отрезков равно коэффициенту подобия.

BC/AD =2,25/9,75 =3/13

BC=3x, AD=13x

Средняя линия трапеции равна полусумме оснований.

(BC+AD)/2 =8 => BC+AD =16 =16x => x=1

BC=3, AD=13

P =3+13+13+13 =42