СРОЧНО ПОМОГИТЕ!!! 90 баллов
Исследуйте функцию y= x^3 − 3lnx на монотонность и экстремумы
Evreika77:
Формулы не прогрузились. Видно только 3-3
y= x^3 − 3lnx
если не сложно, решите это пожалуйста :((( y= 2x^3 − 6x^2 на выпуклость, вогнутость и точки перегиба.
Ответы
Ответ дал:
2
Ответ:
Пошаговое объяснение:
смотри
Приложения:
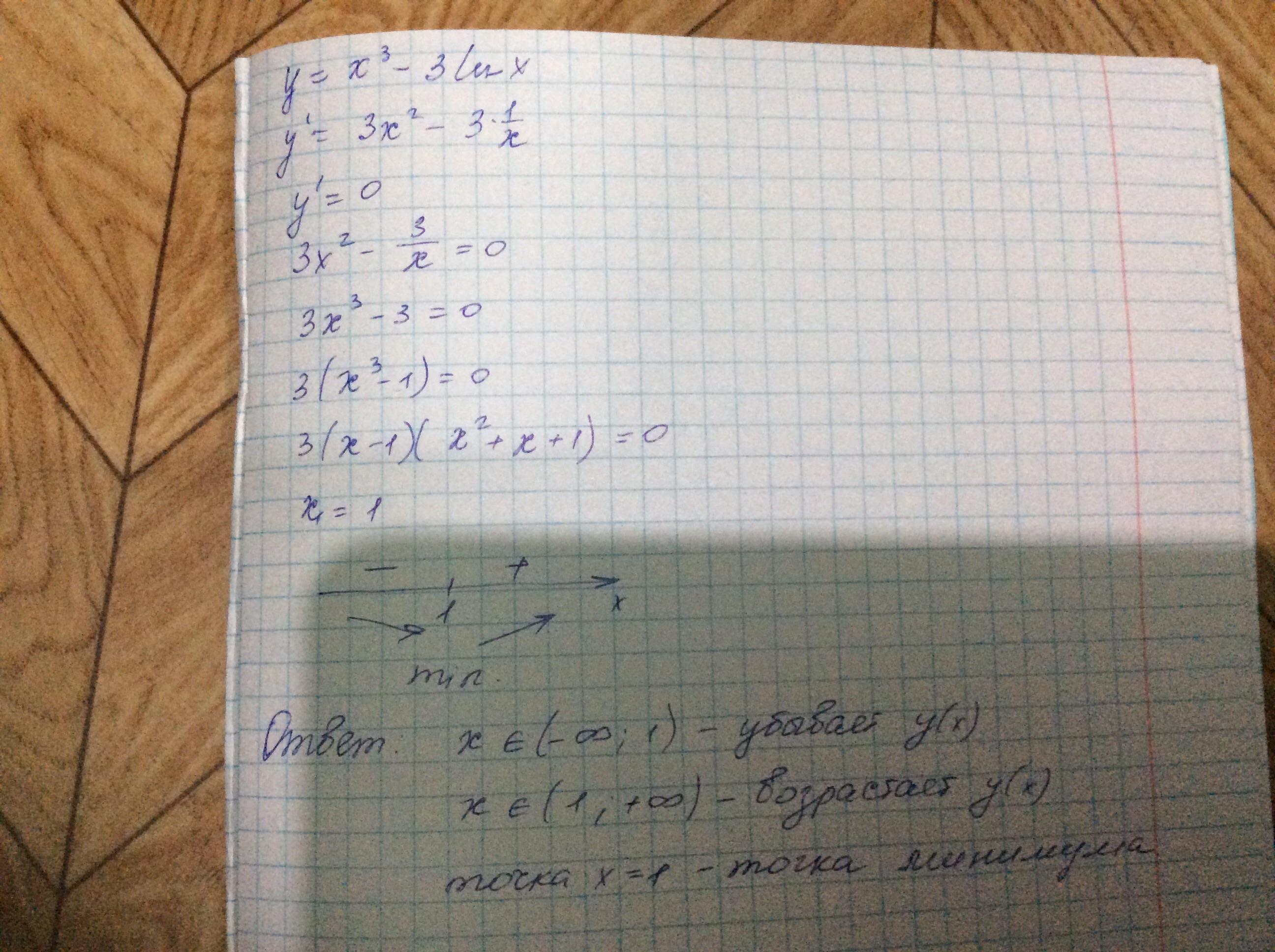
если не сложно, решите это пожалуйста :((( y= 2x^3 − 6x^2 на выпуклость, вогнутость и точки перегиба.
Здравствуйте вы не могли бы вы мне помочь с геометрией пожалуйста
Ответ дал:
2
Пошаговое объяснение:
1.функция определена при х>0
2. найдем производную - она равна 3х²-(3/х)=(3х³-3)/х
3. для нахождения промежутков монотонности и экстремумов решим, например, неравенство (3х³-3)/х>0, оно эквивалентно такому 3* (х³-1)*х>0 приравняем к нулю левую часть 3* (х³-1)*х=0, получим два корня х=0 и х=1, дальше решим неравенство методом интервалов
_______0_____1_____________
+ - +
4.значит, c учетом ОДЗ функции на промежутке (0;1] функция убывает, а на промежутке [1; +∞) функция возрастает,
5. при переходе через точка х=1 производная меняет знак с минуса на плюс, поэтому х=1- точка минимума функции, а сам минимум равен у(1)=1³ − 3ln1=1
Можете мне помочь? Пожалуйста
Здравствуйте вы не могли бы вы мне помочь с геометрией пожалуйста
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад