Question

Решите задачу. Прошу вас ​

Answer 1

Ответ:
х=20°

Решение:
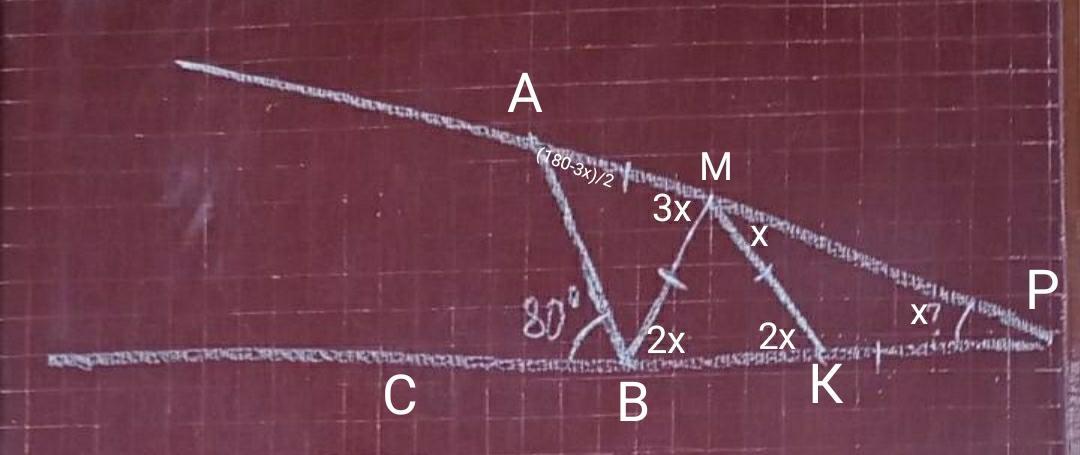
Пусть угол ∠Р будет х°, тогда ∠КМР тоже будет х, т.к. ∆МКР- равнобедренный, углы при основании равны.
∠МКВ- внешний угол треугольника ∆МКР;
Теорема о внешнем угле:
∠МКВ=∠КМР+∠МРК
∠МКВ=х+х=2х.
∠МКВ=∠МВК, т.к. ∆МВК- равнобедренный треугольник.
∠АМВ- внешний угол треугольника ∆МВР.
∠АМВ=∠МВР+∠МРВ, теорема о внешнем угле треугольника.
∠АМВ=2х+х=3х.
∆АВМ- равнобедренный треугольник. Углы при основании равны. ∠МАВ=∠АВМ.
Сумма углов в треугольнике равна 180°.
∠МАВ=(180°-∠АМВ)/2=(180°-3х)/2.
∠СВА- внешний угол треугольника ∆АВР.
∠СВА=∠ВАР+∠АРВ
∠СВА=х+(180-3х)/2
Уравнение:
х+(180-3х)/2=80. |×2
2х+(180-3х)=80*2
2х-3х=160-180
-х=-20
х=20° градусная мера угла ∠Р