Question

СРОЧНО!
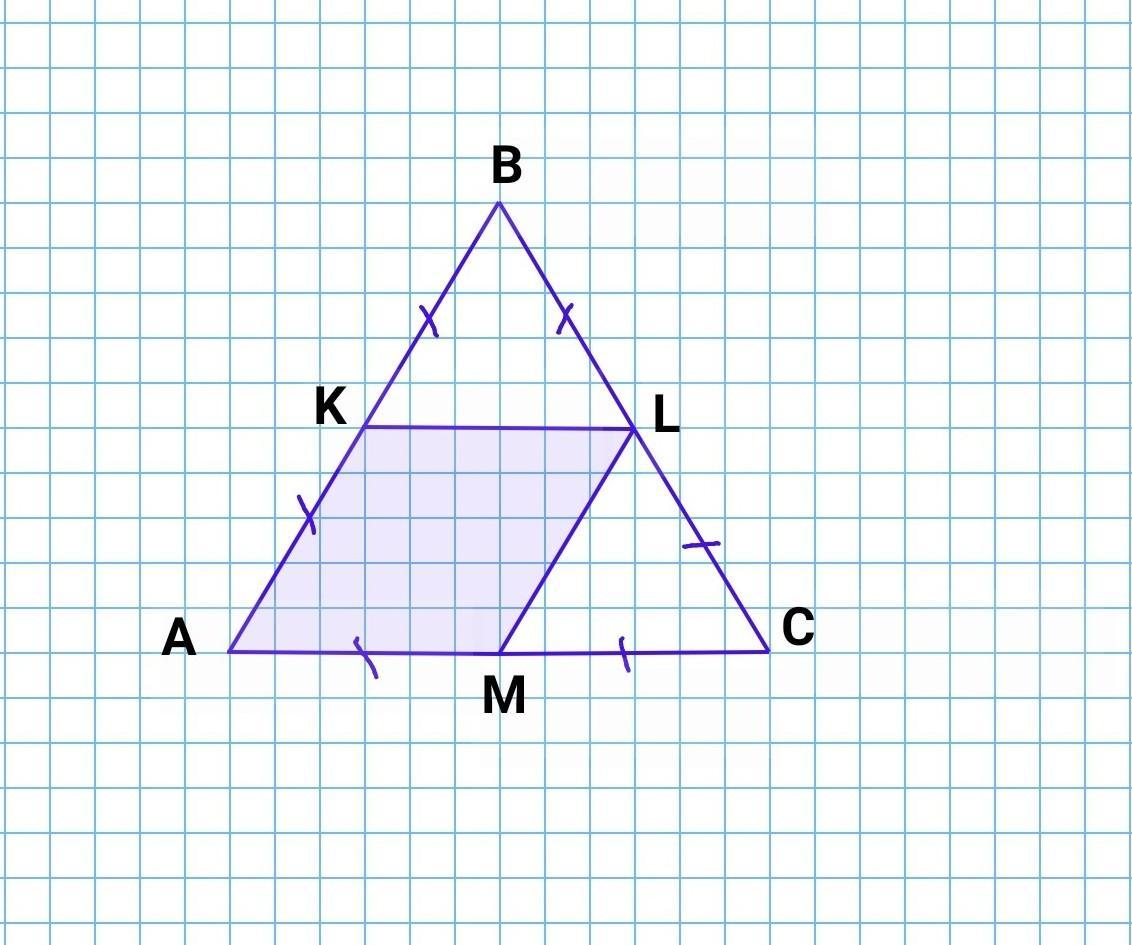
В равностороннем треугольнике ABC отмечены точки K L M, которые являются серединами сторон AB, BC и AC соответственно. Найдите периметр четырёхугольника AKLM, если периметр треугольника KLB равен 21 см. ​

Answer 1

Ответ:

Периметр четырёхугольника AKLM равен 28 см

Объяснение:

Так как ΔАВС - равносторонний, а K, L, M являются серединами сторон АВ, ВС и АС, то

(1) КВ=ВL=LС=МС=АМ=АК - как половины равных сторон.

• Средняя линия треугольника — отрезок, который соединяет середины двух сторон.

⇒ KL, LM, KM - средние линии ΔАВС.

• Средняя линия, соединяющая середины двух сторон треугольника, параллельна третьей стороне и равна её половине:

KL = 1/2 * АС = АМ, но АМ = КВ = BL (1) ⇒ ΔKLB - равносторонний.

По условию периметр ΔKLB = 21:

⇒ КL = KB = BL = 21÷3 = 7 cм

KL II AC, LM II AB (как средние линии), ⇒ AKLM - параллелограмм

• Параллелограмм - это четырехугольник у которого противолежащие стороны попарно параллельны.

LM = 1/2 * АВ = АК

Таким образом: КL=LМ=АМ=АК (1), ⇒ AKLM - ромб.

• Ромб - это параллелограмм, у которого все стороны равны.

Периметр ромба AKLM - равен произведению длины любой его стороны на 4:

Р(AKLM) = 4•KL = 4*7 = 28 см