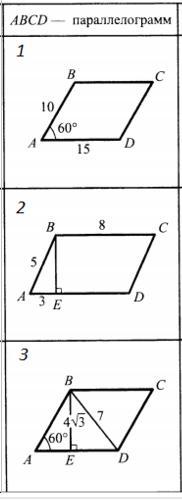
Ответы
Ответ дал:
0
Ответ:
1) 75 2) 32 3)
Объяснение:
1) =AB*AD*sinA,
= 10*15*sin60 = 150*
= 75
2) = AD*BE, BE =
, BE =
= 4, AD = BC = 8
= 8*4 = 32
3) = AD*BE,
ΔABE : прямоугольный, AE =4 : tg60 = 4
ΔBED: прямоугольный, ED = , ED =
= 1
AD = AE + ED, AD = 4 + 1 = 5
= 5 *
=
,
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад