26., Диагонали разбивают четырёхугольник на четыре
треугольника. Докажите, что произведение площадей двух
треугольников, прилегающих к его противоположным
сторонам, равно произведению площадей двух других
треугольников.
Ответы
Ответ дал:
0
Ответ:
СМ НИЖЕ
Объяснение:
Если у двух треугольников есть равные высоты или они совпадают, то их площади относятся как основания, к которым проведены сами высоты.
=
,
=
,
=
,
=
=
,
=
⇒
=
⇒ S₁•S₃ = S₂•S₄
ЧТД
Приложения:
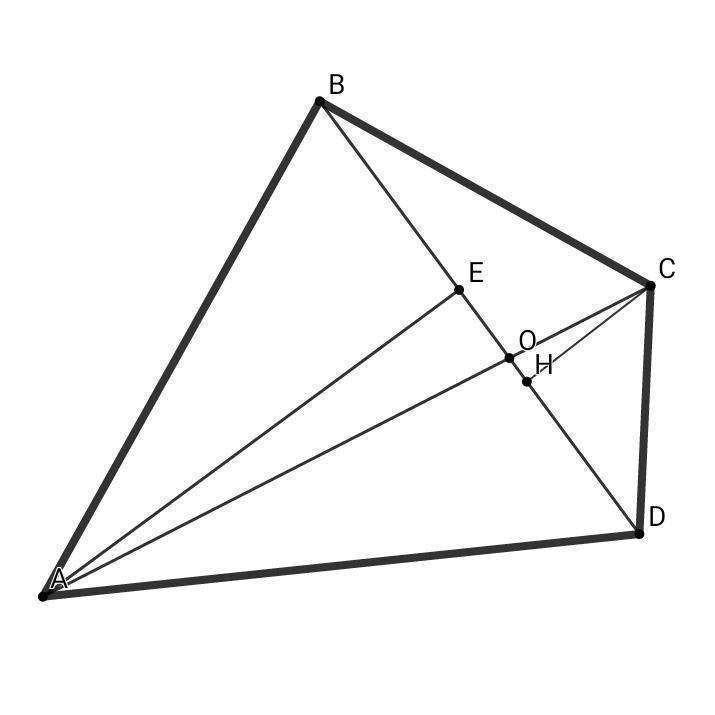
55555555552187:
отметь короной, плиз, тебе не трудно, а мне приятно, я так старался для тебя!!!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад