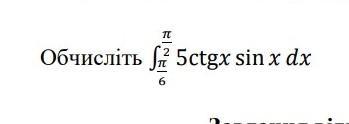Ответы
Ответ дал:
2
Ответ:
2.5
Пошаговое объяснение:
Для начала, вычислим первообразную:
∫(5ctg(x)sin(x))dx = 5∫(ctg(x)sin(x))dx
Но ведь ctg(x) * sin(x) = (cosx/sinx) * sinx = cosx
Тогда, весь наш интеграл - это просто 5∫(cos(x))dx.
Но первообразная от косинуса - это синус! А значит, наша первообразная равна 5sin(x)
Т.к. интеграл определенный, применим формулу Ньютона-Лейбница (определенный интеграл от f(x) с нижним пределом a и верхним пределом b равен F(b) - F(a), где F(x) - первообразная функции f(x))
Подставляем, получаем 5sin(pi/2) - 5sin(pi/6) = 5 - 2.5 = 2.5
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад