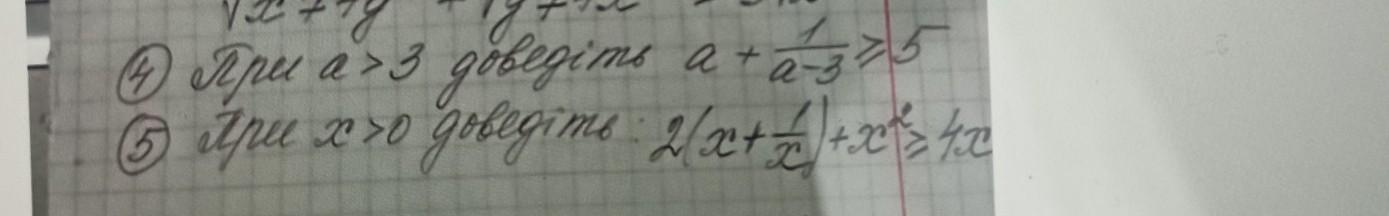Ответы
Ответ дал:
1
Ответ:
Объяснение:
4) a>0
неравенство верно
в числителе квадрат любой величины ≥ 0
в знаменателе a-3>0 , поскольку а>3
исходное неравенство тоже верно
5) x>0
сумма взаимно обратных положительных чисел ≥ 2
x + 1/x ≥ 2
неравенство верно
квадрат любой величины ≥ 0
тождества доказаны
Tdvbg:
Спасибо большое)
:)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад