основание кругового сегмента равна 12 , а дуга равна 120 градусов. Найдите площадь этого кругового сегмента.
Помогите пожалуйста!
Ответы
Ответ дал:
1
Ответ:
≈29,45 см²
Объяснение:
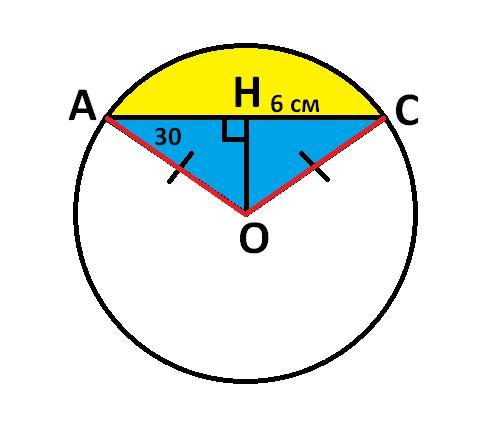
Площадь сектора, не сегмента!!! круга равна a*пR²/360 где a=угол, R=радиус,
п=число пи; S AC=120*пR²/360=(1/3)пR²
Теперь нужно найти радиус. Проведём высоту, радиусы AO=OC, значит она делит сторону 12 в основании пополам, угол A=30°; 2OH=AO; возьмём OH=x; тогда по теореме Пифагора имеем:
(2x)²=6²+x²; 4x²=6²+x²; 4x²-x²=36; 3x²=36; x²=12; x=√12=2√3 (длина не может быть отрицательной). AO=2x=4√3; S AC=(1/3)(4√3)²*3,14
S AC=3,14*48/3=50,24 см²
Теперь высчитаем площадь треугольника AOC;
S=(12*OH)/2=6*2√3=12√3
Площадь кругового сегмента равна 50,24-12√3≈29,45 см²
Приложения:
Аноним:
а может получится ответ 16П-12√3?
16П=50,24
Так что может.
у тебя то есть всё правильно да?
Прочитай внимательно, я всё логично выстроил и доказал.
Да.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад