Предмет: Геометрия
Автор: ggfgyyff5655
Вопрос задан 7 лет назад

Срочно нужна помощь с Геометрией, 11 класс!!!
В усечённый конус, радиусы оснований которого равны 12 и 27, вписан шар. Найдите радиус этого шара. Требуется решение с формулами.

Simba2017: тогда высота трапеции-это диаметр шара, ищите по пифагору

Simba2017: h=36;R=18

ggfgyyff5655: Все понял, кроме Пифагора. Какие значения туда подставлять? Под корнем должна быть разность квадратов боковой стороны и большего/меньшего радиусов основания?

Simba2017: нет

Simba2017: h^2=39^2-15^2

Simba2017: 15=(54-24)/2

Simba2017: да, верно вы написали...

ggfgyyff5655: А что такое 15? К чему это значение относится? Это не высота, не радиус, не боковая сторона. Тогда что это?

Simba2017: это разница радиусов по вашему

ggfgyyff5655: Вас понял. большое спасибо за помощь.

Ответы

Ответ дал: ShadowLisenok

Ответ:

Объяснение:

Шар можно вписать в усечённый конус, если сумма оснований трапеции, которая является осевым сечением усечённого конуса, равна сумме боковых сторон, которые равны, так как являются образующими конуса: AD+BC=AB+CD; AD+BC=2AB. r=27; r1=12;

AD=2*27; BC= 2*12 (потому что диаметры оснований.)

2*27 + 2*12 = 2AB => 27+12=AB => AB=39;

HH1=BH2= $\sqrt{AB^{2}-AH_{2} ^{2} }$ ;

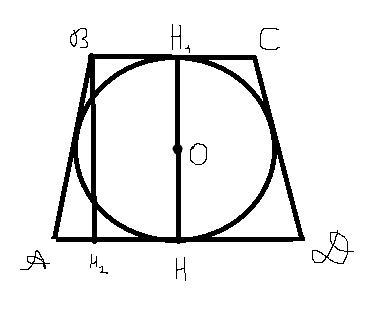
AH2= AH-BH1= 27-12=15 (На чертеже должно быть понятно что это);

$BH_{2} =\sqrt{AB^{2} -AH_{2} ^{2} } \\ BH_{2} =\sqrt{1521-225} =36$

Как видно на чертеже, высота усечённого конуса - это диаметр окружности, вписанной в осевое сечение данного конуса, следовательно радиус шара равен:

R= $\frac{1}{2} *36=18$