Question

ПОМОГИТЕ ПОЖАЛУЙСТА, ДАЮ 40 БАЛЛОВ!!!!!!

Дан прямоугольный треугольник ABC с прямым углом C . AC = 15 , ∠A = 60
∘
Найди длину окружности, описанной около этого треугольника.

Запиши в поле ответа значение, поделённое на π

Answer 1

Ответ:

30

Объяснение:

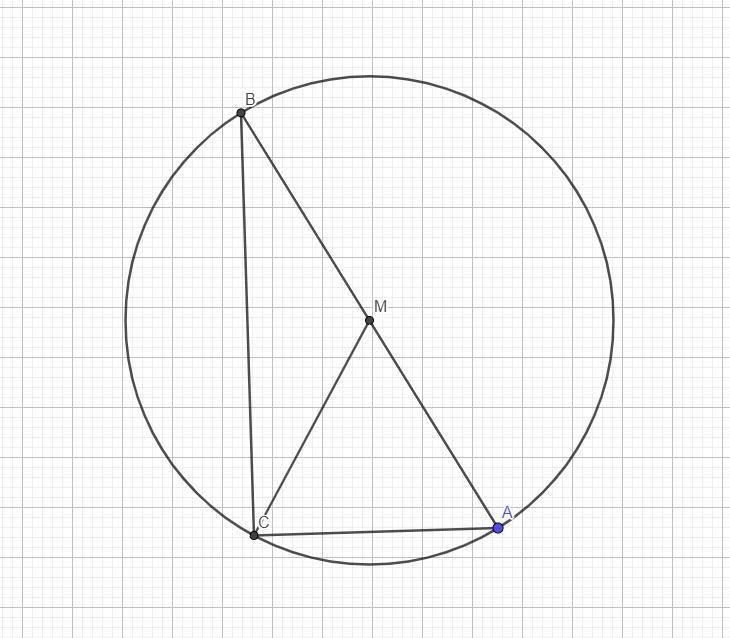
Раз ∠A = 60, то ∠B = 90 - 60 = 30. И этот угол лежит как раз напротив AC, а как известно катет прямоугольного треугольника, лежащий напротив угла 30 градусов равен половине гипотенузы! Также известно, что центр описанной окружности прямоугольного треугольника всегда лежит на середине гипотенузы. (т.к. медиана проведенная к этой самой гипотенузе равна ее половине) Значит наша гипотенуза равна 15 × 2 = 30, а радиус описанной окружности равен ее половине, т.е. 15. Тогда диаметр равен 30 и длина окружности равна 30π, а раз в ответе нужно записать число деленное на π, то ответ: 30.

P.s. приложил рисунок, на нем CM - медиана.