Найти общее решение (общий интеграл) дифференциального уравнения первого порядка, надо подробное решение))
Приложения:
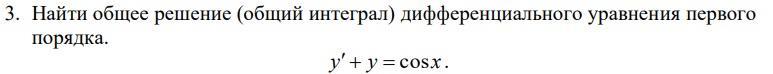
Ответы
Ответ дал:
1
1 СПОСОБ (Метод Лагранжа).
Произвольную постоянную примем за функцию от .
Подставим и
в исходное уравнение:
Отдельно найдем полученный неопределенный интеграл:
Отсюда получаем что:
Отсюда получаем что:
Теперь подставим в формулу :
В итоге окончательно получаем:
2 СПОСОБ (Метод Бернулли)
Пусть тогда:
потребуем, чтобы
тогда:
Подставим найденное значение в
:
В предыдущем способе данный интеграл был найден методом интегрирования по частям, поэтому не будет здесь его искать а просто подставим уже найденный.
но
тогда:
Отсюда получаем:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад