Question

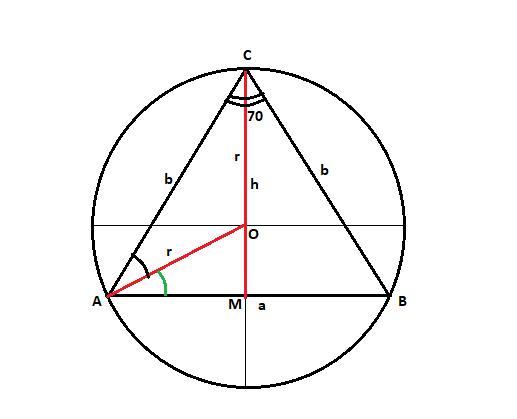
У коло радіуса 5 см вписано рівнобедрений трикутник із кутом між бічними сторонами 70°. Знайти висоту, прове­дену до основи, та бічну сторону трикутника.

Answer 1

Ответ:

b ≈ 8,2 см; h = 6,71 см

Объяснение:

В круг радиусом 5 см вписан равнобедренный треугольник с углом между боковыми сторонами 70° (∠ACB обозначен двойной).

Найти высоту, проведённую из этого угла до основания, и боковую сторону треугольника.

Решение:

Смотрите рисунок.

CM - это высота, медиана и биссектриса треугольника ABC.

Значит, ∠ACM = ∠ACB / 2 = 70°/2 = 35°.

Треугольник AOC - равнобедренный, OA = OC = r = 5 см

∠AOC = 180° - 35° - 35° = 110°

∠OAC = ∠ACO = 35° (∠OAC обозначен черным)

∠CAB = ∠CBA = (180° - 70°) / 2 = 110° / 2 = 55°

∠OAM = ∠CAB - ∠OAC = 55° - 35° = 20° (обозначен зеленым)

Из прямоугольного треугольника OAM получаем:

AM = a/2 = OA*cos (OAM) = 5*cos 20° ≈ 4,7 см

Из равнобедренного треугольника AOC по теореме косинусов:

AC^2 = OA^2 + OC^2 - 2*OA*OC*cos (AOC)

AC^2 = 5^2 + 5^2 - 2*5*5*cos 110° = 25 + 25 - 2*25*cos 110° =

= 50*(1 - cos 110°) ≈ 50*1,342 = 67,1

Боковая сторона треугольника ABC:

b = AC = √67,1 ≈ 8,2 см

Из прямоугольного треугольника ACM по теореме Пифагора:

CM^2 = AC^2 - AM^2 = 67,1 - (4,7)^2 = 67,1 - 22,09 = 45,01

Высота треугольника ABC, опущенная на основание:

h = CM = √45,01 ≈ 6,71 см