Question

CРОЧНО, ПОЖАЛУЙСТА, ОТДАМ ВСЕ БАЛЛЫ!!! упростить выражение cos(pi+a)

Answer 1

Відповідь:

1. cos($\pi +\alpha$)=$-cos\alpha$.
2. $cos(3\pi +\alpha )+sin(\frac{\pi }{2} +\alpha )=cos(\pi +\alpha )+sin\alpha =-cos\alpha +sin\alpha =sin\alpha -cos\alpha .$
3. $\frac{cos(2\pi -\alpha )}{sin(-\alpha )} *\frac{sin(\pi -\alpha )}{tg(\frac{3\pi }{2} +\alpha )} =\frac{cos\alpha }{-sin\alpha}*\frac{sin\alpha }{-tg\alpha }=\frac{cos\alpha*cos\alpha }{sin\alpha } =cos\alpha ctg\alpha .$

Пояснення: зведення виконувалися згідно з такими правилами (кут $\alpha$ вважаэмо гострим, тобто $0\leq \alpha \leq \frac{\pi }{2}$):

1. Якщо під знаком перетворюваної тригонометричної функції міститься сума аргументів виду π+t,π−t,2π+t,2π−t, тоді найменування тригонометричної функції слід зберегти;

2. Якщо під знаком перетворюваної тригонометричної функції міститься сума аргументів виду π2+t,π2−t,3π2+t,3π2−t, тоді найменування тригонометричної функції слід змінити (sin↔cos; tg↔ctg);

3. Перед отриманою функцією аргументу t треба поставити той знак, який мала б функція, що перетворюється, за умови, що 0<t<π2.

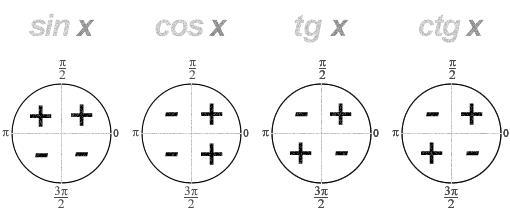
На зображенні знаки тригонометричних функцій відповідно до величини кута в дужках.