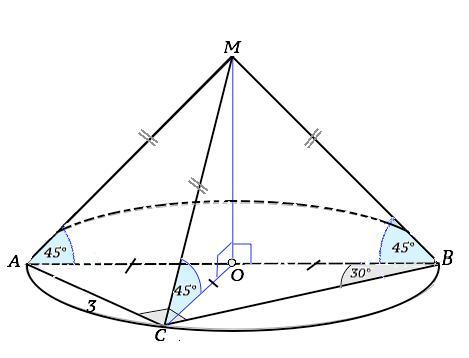
Боковые рёбра пирамиды наклонены к плоскости основания под углом 45˚. Основанием пирамиды служит прямоугольный треугольник со стороной, равной 3, и противоположным углом 30˚. Найдите объём описанной около пирамиды конуса.
а) Определить нельзя; б) 3π см3; в) 2π см3; г) 18π см3; д) 9π см3.
Ответы
Ответ: 9π см³
Объяснение: Если основание пирамиды - прямоугольный треугольник, а боковые рёбра наклонены к плоскости основания под равным углом, то её высота проходит через центр описанной около основания окружности, т.е. через середину гипотенузы.
* * *
Пусть в пирамиде МАВС угол С ∆ АВС - прямой, МО - высота пирамиды ( МО - перпендикуляр к плоскости основания), и углы МАО=МВО=МСО=45°.
Тогда ∆ МАО=∆ МВО=∆ МСО по равному острому углу и общему катету МО. Они равнобедренные, МО=АО=ВО=СО=R.
Катет АС противолежит углу 30° => равен половине гипотенузы АВ.
АВ=2•3=6.
Конус, описанный около пирамиды, имеет общую с ней вершину, боковые ребра - образующие конуса, а его основание - описанная около основания пирамиды окружность.
R=3.
Формула объёма конуса V=S•h:3, где S - площадь основания конуса, h- его высота.
V=πR²•h:3= π•3²•3:3=9π см³