1035. Найдите все целые числа, являющиеся решениями системы неравенств:
Вся информация в фото. Пожалуйста, помогите!
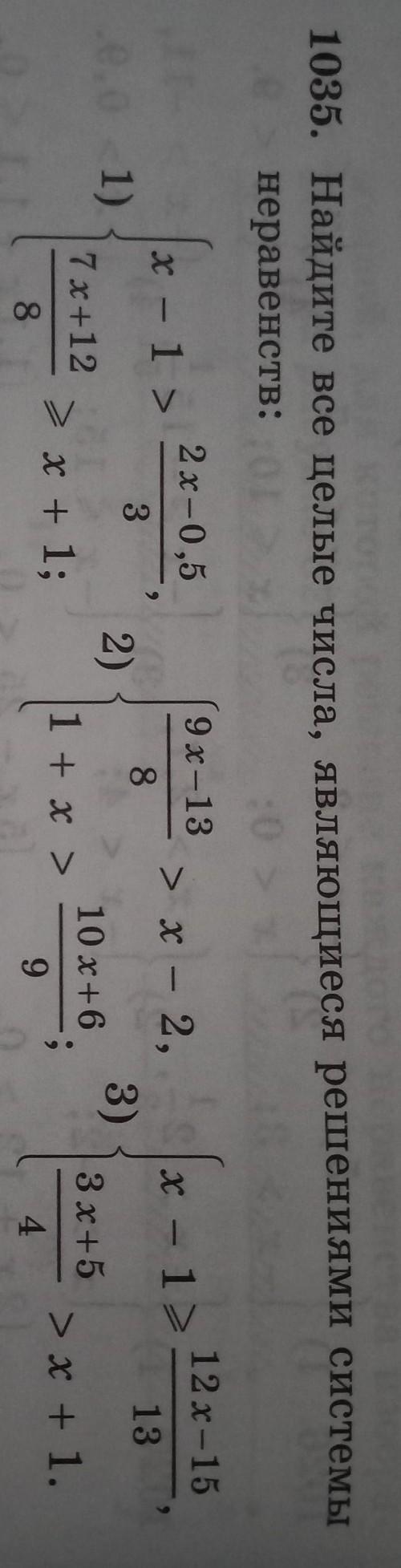
Ответы
Ответ:
Целые числа, являющиеся решениями системы неравенств:
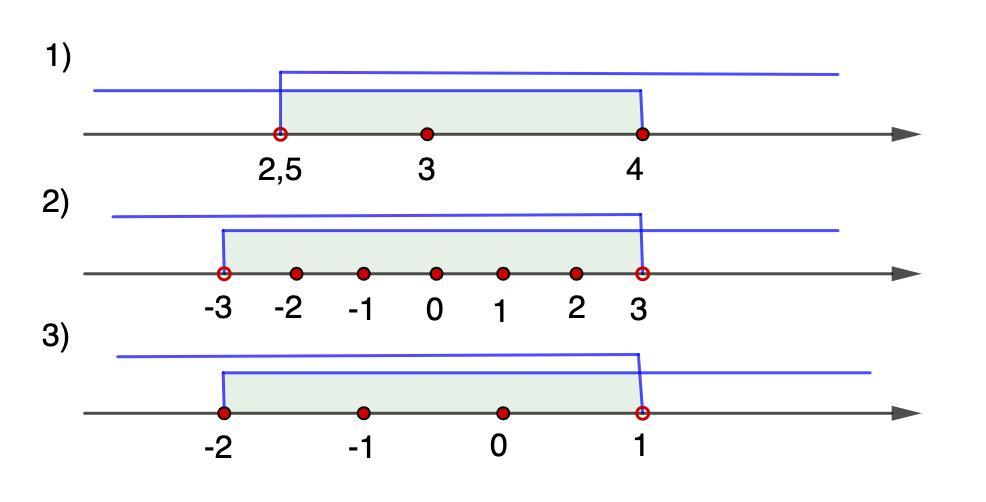
1) 3, 4;
2) -2, -1, 0, 1, 2;
3) -2, -1, 0.
Пошаговое объяснение:
Требуется найти все целые числа, являющиеся решениями системы неравенств.
1)
- Если обе части неравенства умножить или разделить на положительное число, то получим неравенство, равносильное данному.
- Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный.
- Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства перевернется.
Получим:
x ∈ (2,5; 4]
Второе неравенство нестрогое, поэтому 4 входит в решение.
Целые числа, являющиеся решениями системы неравенств, равны: 3, 4.
2)
Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный. Приведем подобные члены и решим неравенства:
x ∈ (-3; 3)
Неравенство строгое, поэтому (-3) и 3 не входят в решение.
Целые числа, являющиеся решениями системы неравенств, равны: -2, -1, 0, 1, 2.
3)
Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный. Приведем подобные члены и решим неравенства:
x ∈ [-2; 1)
Первое неравенство нестрогое, поэтому (-2) входит в решение.
Целые числа, являющиеся решениями системы неравенств, равны: -2, -1, 0.