Question

Пожалуйста помогите!!!

Answer 1

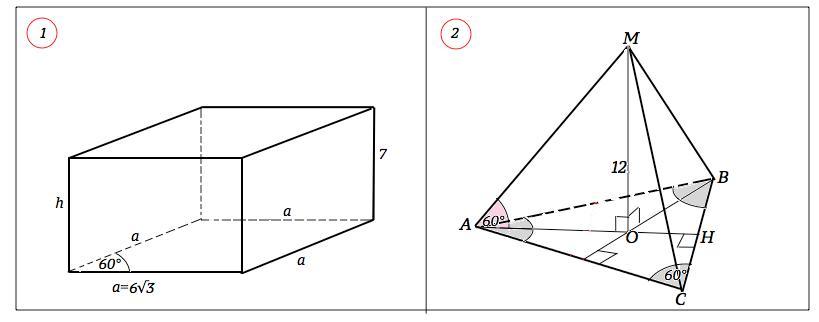
1)  Основанием прямого параллелепипеда является ромб со стороной 6√3 см и углом 60°. Боковое ребро параллелепипеда равно 7 см. Найдите объём параллелепипеда (к задаче выполните рисунок и запишите решение, опираясь на известные формулы)

-------

  В прямом параллелепипеде боковые ребра   перпендикулярны основанию и равны его высоте.

  Формула объёма параллелепипеда

                    V=S•h,

где Ѕ – площадь основания параллелепипеда, h - его высота.

Одна из формул площади параллелограмма

S=a•b•sin α, где а и b -  стороны,  α - угол между ними.

  Ромб - параллелограмм с равными сторонами. =>

                 S=a²•sinα

S=(6√3)²•√3•1/2=54√3 см²

V=54√3•7=378√3 см³

                               *    *    *

2)    В правильной треугольной пирамиде боковые рёбра образуют с плоскостью основания углы по 60°. Найдите объём пирамиды, если её высота 12 см. (К задаче выполните рисунок, обоснуйте угол между прямой и плоскостью, запишите решение, опираясь на известные формулы,  теоремы, следствия из них)

—————

Формула объёма пирамиды V=S•h/3, где Ѕ – площадь основания пирамиды, h – её высота.

Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.

Пусть основание пирамиды АВС, МО - её высота.

   Угол между прямой и плоскостью — это угол между прямой и её проекцией на данную плоскость.

АН – высота ∆ АВС, перпендикулярна ВС и содержит проекцию  АО наклонной МА. => <МАН=60° ( по условию).

Из прямоугольного АОМ АО=МО:tg60°=12/√3=4√3

О - центр основания правильного треугольника  и делит его высоту в отношении АО:ОН=2:1. => АН=4√3+0,5•4√3=6√3

Все углы правильного треугольника =60°

ВС=АН:sin60°=6√3:(√3:2)=12

Формула площади правильного треугольника

S=(a²√3):4 =>

V=(144√3:4)•12:3=144√3 см³