Ответы
Ответ дал:
1
Ответ:
3/2
Пошаговое объяснение:
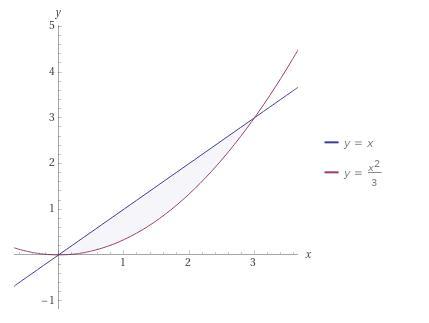
Графики выглядят следующим образом (во вложениях)
Тогда закрашенная площадь и есть искомая, найти её можно при помощи интеграла:
Здесь f2(x) - это верхняя функция, а f1(x) - нижняя
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад