Известно, что график функции y = ax(квадрат) – 3х + 6 проходит через
точку (9; 6). Найдите расстояние между точками числовой прямой,
Координаты которых нули этой функции.
Приложения:
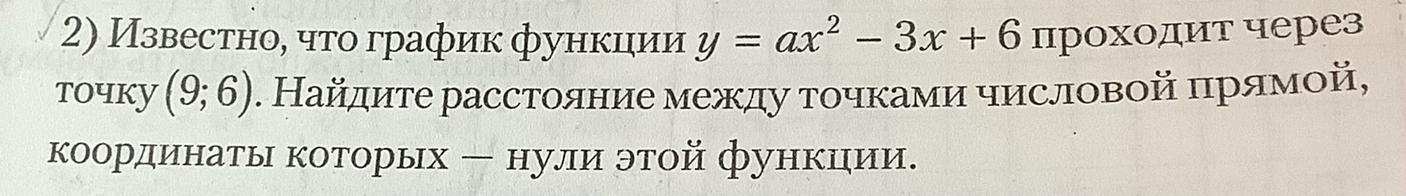
Ответы
Ответ дал:
1
Ответ:
Объяснение:
подставим (9; 6) в уравнение y = ax²– 3х + 6 и найдем а
6 = a*9²– 3*9 + 6
6 = 81a– 27 + 6
81a– 27=0
81a=27 ; a=27/81
a=1/3
подставим a=1/3 в уравнение y = (1/3)x²– 3х + 6 и найдем нули
у=(1/3)x²– 3х + 6 =0
(1/3)x²– 3х + 6 =0 умножим на 3
x²– 9х + 18 =0
по теореме Виета корни х₁=3 х₂=6
расстояние между между точками числовой прямой,
координаты которых нули этой функции R=6-3=3
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад