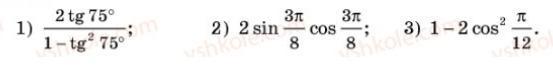Ответы
Ответ дал:
1
Ответ:
Объяснение:
Применим формулу тангенса двойного угла ,у отнимая период получаем тангенс отрицательного угла. Зная,что тангенс нечетная функция , выносим минус перед тангенсом и получаем ответ.
Используем тождество,что синус 180- угол и синус самого угла равныф по величине и знаку.
Используем формулу косинуса двойного угла,предварительно вынесем за скобку минус,поскольку у нас в примере противоположные формуле знаки.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад