с у 3.32. Докажите, что биссектрисы острых углов прямо- угольного треугольника пересекаются под углом 45. Al ро цаашите углы прямоугольного треуго. пожалуйста срочно скиньте фото как решается
Приложения:

Ответы
Ответ дал:
4
Ответ:
Доказано, что биссектрисы острых углов прямоугольного треугольника пересекаются под углом 45°.
Объяснение:
Требуется доказать, что биссектрисы острых углов прямоугольного треугольника пересекаются под углом 45°.
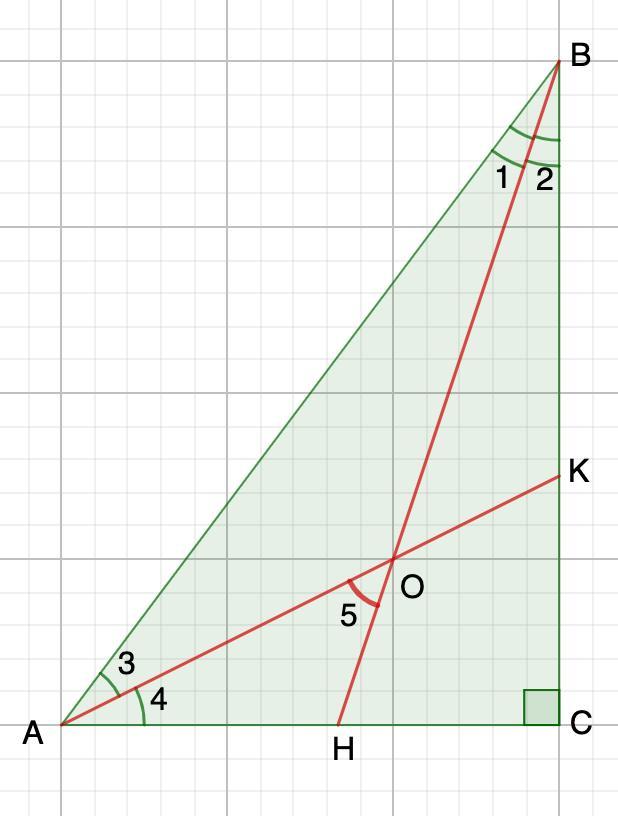
Дано: ΔАВС - прямоугольный;
АК и ВН - биссектрисы;
Доказать: ∠АОН = 45°
Доказательство:
Рассмотрим ΔАВС - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠А + ∠ В = 90°
или
∠1 +∠2 + ∠3 + ∠4 = 90°
∠1 = ∠2 (ВН - биссектриса)
∠3 = ∠4 (АК - биссектриса)
(∠1 + ∠3) + (∠2 + ∠4) = 90°
⇒ ∠1 + ∠3 = ∠2 + ∠4 = 90° : 2 = 45°
- Внешний угол треугольника равен сумме двух углов, не смежных с ним.
⇒ ∠АОН = ∠1 + ∠3 = 45° (внешний ΔАВО)
Что и требовалось доказать.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад