Кайрат любит играть в футбол. Во время игры футбольный мяч оказался у Кайрата, который расположился на расстояниях 12 м от одной штанги ворот и 14 м от другой. Ширина ворот 7 м. Найдите косинус угла попадания мяча в ворота.
Ответы
Ответ дал:
1
Ответ:
Косинус угла попадания Кайратом футбольного мяча в ворота равен
Объяснение:
Найти косинус угла попадания Кайратом футбольного мяча в ворота шириной 7 м, который находится на расстоянии 14 м и 12 м от штанг ворот.
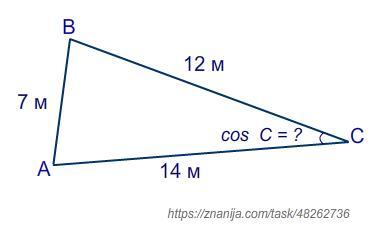
Обозначим места расположения стоек ворот точками A и B, место расположения Кайрата - точка С.
Точки ABC являются вершинами треугольника ABC. Угол C - угол попадания мяча в ворота.
Дано:
AB = 7 м;
AC = 14 м;
BC = 12.
Найти: cos C.
Решение.
- Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
a² = b² + c² - 2bc·cosα.
1) Применим к треугольнику теорему косинусов, по ней найдем косинус угла C.
В ΔABC:
AB² = AC² + BC² - 2 · AC · BC · cos C ⇒
2) Подставим наши значения.
Косинус угла попадания Кайратом футбольного мяча в ворота равен
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад