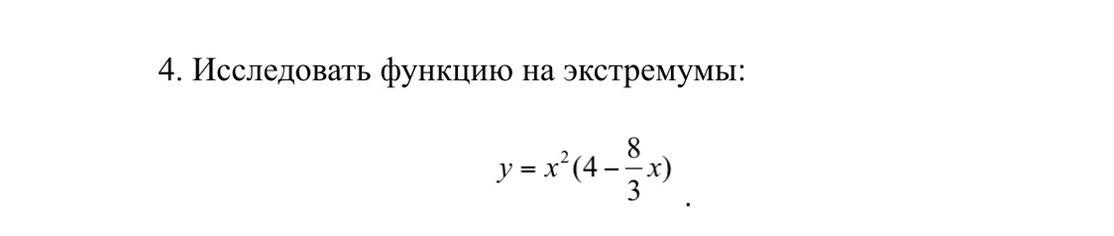Ответы
Ответ дал:
1
Ответ:
Экстремумы функции:
х min = 0
x max = 1
Пошаговое объяснение:
Требуется исследовать функцию на экстремумы.
Найдем производную:
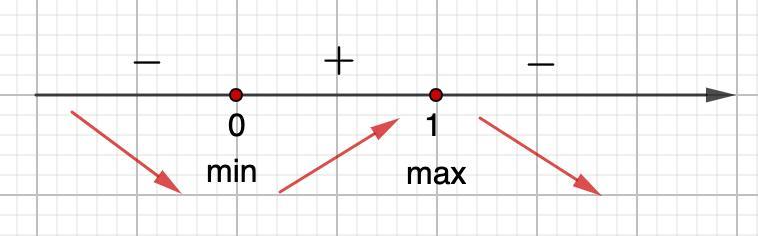
Приравняем к нулю и найдем корни. Отметим их на числовой оси. Определим знак производной на промежутках.
y' = 0
8x - 8x² = 0
8x· (1 - x) = 0
x = 0 или х = 1
Функция возрастает на промежутке [0; 1]
Функция убывает на промежутках (-∞; 0]; [1; +∞)
- Если производная меняет знак с минуса на плюс, то в этой точке будет минимум.
⇒ х min = 0
- Если производная меняет знак с плюса на минус, то в этой точке будет максимум.
⇒ x max = 1
Использовали формулы:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад