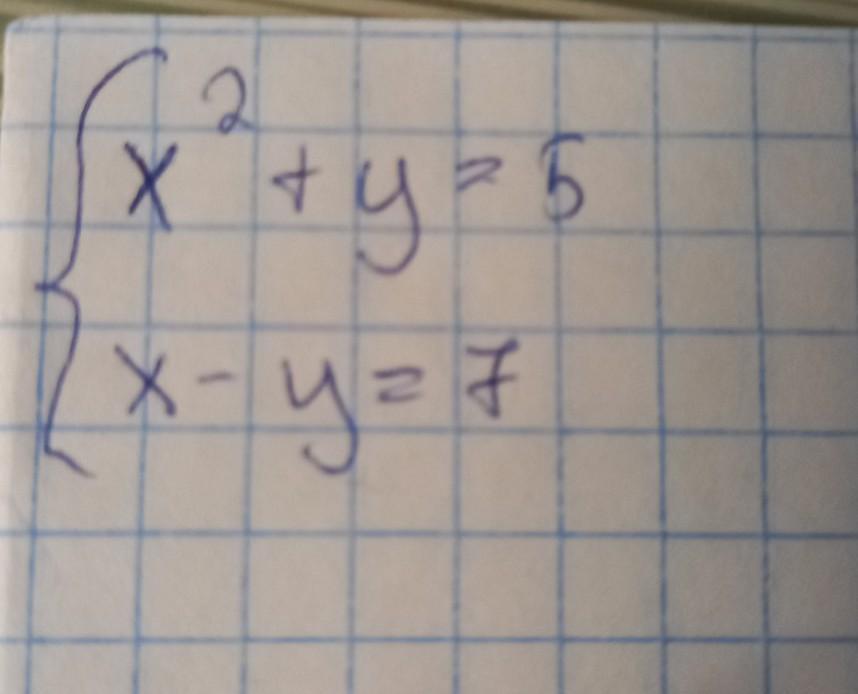Ответы
Ответ дал:
1
Объяснение:
y=5-x^2
x-(5-x^2)=7
x-5+x^2=7
x^2+x-12=0
x1= 3
x2= -4
Подставляем x1,x2 в y=5-x^2
y1=5-9=-4
y2=5-16=-11
ОТВЕТ: (x1;y1)=(3;-4)
(x2;y2)=(-4;-11)
Ответ дал:
1
Ответ:
x₁ = 3, y₁ = -4, x₂=-4, y₂=-11
Объяснение:
д = b²-4ac = 1+48 = 49
x₁,₂ = -b₋⁺√Д/2
x₁ = -1+7/2 = 3
x₂ = -1-7/2 = -4
y₁ = 3-7 = -4
y₂ = -4-7 = -11
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад