Question

знайдіть площу трикутника, якщо його діагоналі дорівнюють 2 см і 3 см, а кут між ними 150 градусов
СРОЧНО ПОМОГИТЕ ​

Answer 1

S=2*3/2=3 см в квадрате

по формуле площадь треугольника s=a*b/2

Answer 2

Ответ:

Площадь четырехугольника = 1,5 см²

Объяснение:

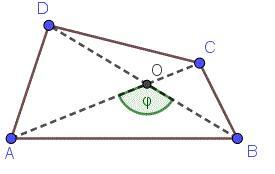
Площадь произвольного четырехугольника можно найти перемножив диагонали данного четырехугольника, полученный результат разделить на 2, и это всё умножить на синус любого из четырёх углов между ними.

$S = \frac{1}{2} AC*BD*sin(f)$

Т.к. вычислять sin(150°) на первый взгляд сложновато, а смежный угол с 150° это 180° - 150° = 30° ⇒ sin(30°) = 1/2

⇒ $S = \frac{1}{2} *2*3*\frac{1}{2} = \frac{3}{2} = 1,5 cmв$