Question

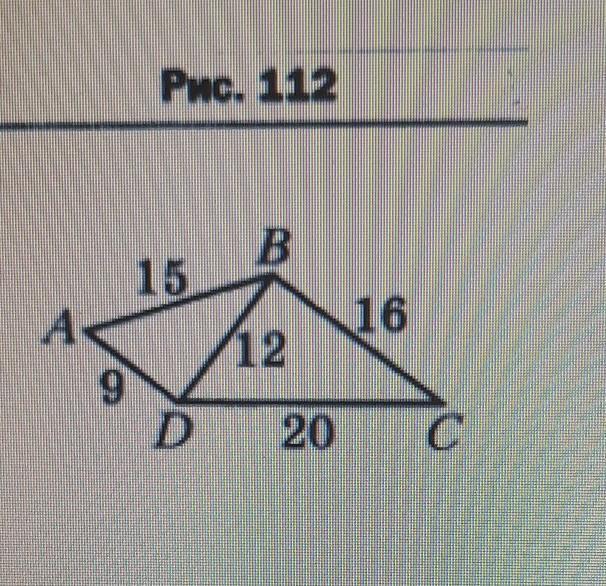
Подобны ли треугольники ABD и BDC, изображённые на рисунке 112 (длины отрезков даны в сантиметрах)?
СРОЧНО​

Answer 1

Ответ: да, подобны.

Пошаговое объяснение:

Проверим подобие ΔBDA и ΔCBD по III признаку подобия треугольников:

• Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

То есть должно быть следующее равенство:

$\dfrac{AB}{CD} = \dfrac{AD}{BD} = \dfrac{BD}{BC}$

$\dfrac{AB}{CD} = \dfrac{15}{20} = \dfrac{3}{4}$

$\dfrac{AD}{BD} = \dfrac{9}{12} = \dfrac{3}{4}$

$\dfrac{BD}{BC} = \dfrac{12}{16} = \dfrac{3}{4}$

⇒ $\triangle BDA \sim \triangle CBD$, по III признаку подобия треугольников.