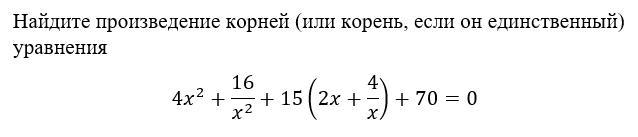Ответы
Ответ дал:
2
Сделаем замену
Тогда
Получим уравнение
Обратная замена
Ответ: 4
14Fan:
МНЕ ПОМОГИТЕ ПОЖАЛУЙСТА ВОПРОС В ПРОФИЛЯ
помогите пожалуйста с геометрией, задание в профиле
очень нужно, пожалуйста
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад