Question

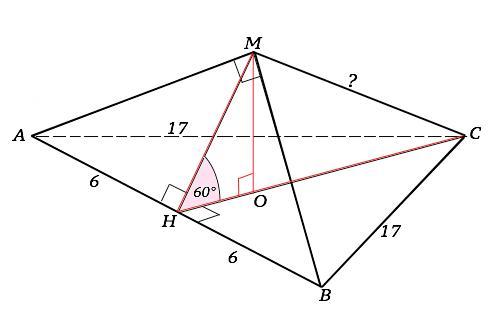
Точка М не лежит в плоскости АВС. АВС-равнобедренный треугольник с основанием АВ, АМВ- прямоугольный треугольник с прямым углом АМВ. АС=ВС=17, АВ=16, угол между (АВС) и (АВМ) равен 60°. Найти МС

Answer 1

Ответ:

Объяснение:

  Проведем в ∆ АСВ из вершины С прямую перпендикулярно к АВ до пересечения с ней в точке Н.  По условию  АС=ВС=17, => СН - высота и медиана ∆ АСВ. Наклонная МН⊥АВ ( по т. о 3-х перпендикулярах), АН=НВ=16:2=8.

МН - высота и медиана ∆ АМВ.

∆ АМВ  - прямоугольный ( дано) и равнобедренный ( из свойств равнобедренного тр-ка). Медиана прямоугольного треугольника равна половине гипотенузы. => МН=АН=ВН=8.

    В  ∆ СНВ по т. Пифагора СН=√(АС²-ВН²)= √(17²-8²)=15.

В ∆ МНС известны две стороны и угол между ними.

По т.косинусов МС=√(СН²+МН²-2•СН•МН•cos60°).

МС=√(15^2+8^2-2•8•15•1/2)=13 (ед. длины)  

Тот же результат получим, если из М опустим на СН высоту ∆ МНС. ОН =МН•cos60°=4. Дальнейшие вычисления без труда сможете выполнить самостоятельно.